题目内容
已知 中,点A、B的坐标分别为
中,点A、B的坐标分别为 ,点C在x轴上方。
,点C在x轴上方。
(1)若点C坐标为 ,求以A、B为焦点且经过点C的椭圆的方程;
,求以A、B为焦点且经过点C的椭圆的方程;
(2)过点P(m,0)作倾角为 的直线
的直线 交(1)中曲线于M、N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值。
交(1)中曲线于M、N两点,若点Q(1,0)恰在以线段MN为直径的圆上,求实数m的值。
【答案】
(1)椭圆方程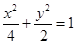 ;(2)
;(2)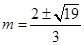
【解析】
试题分析:(1)由已知可知椭圆焦点在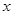 轴上且
轴上且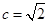 ,设椭圆的标准方程
,设椭圆的标准方程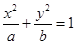 ,在利用椭圆的定义求
,在利用椭圆的定义求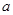 ,根据
,根据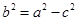 可求
可求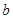 ;
;
(2)直线的倾斜角为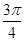 可知斜率为
可知斜率为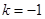 ,设点斜式的直线方程
,设点斜式的直线方程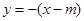 ,因为点
,因为点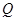 在以线段
在以线段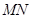 为直径的圆上,所以
为直径的圆上,所以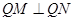 ,即
,即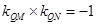 ,联立直线与椭圆方程,利用韦达定理建立关于
,联立直线与椭圆方程,利用韦达定理建立关于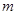 的等式,可求得
的等式,可求得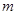 的值.
的值.
试题解析:(1)设椭圆方程为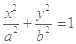 ,c=
,c=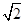 ,2a=
,2a=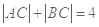 ,b=
,b=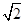 ,椭圆方程为
,椭圆方程为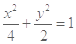 .
.
(2)直线l的方程为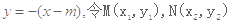 ,联立方程解得
,联立方程解得
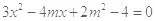 ,
,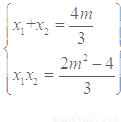 ,若Q恰在 以MN为直径的圆上,
,若Q恰在 以MN为直径的圆上,
则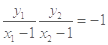 ,即
,即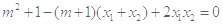 ,
,
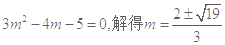 .
.
考点:1、椭圆的定义、椭圆的标准方程;2、直线方程,圆中直径所对的圆周角为直角;3、直线与椭圆的位置关系、韦达定理.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (a >0)与x轴的正半轴交于点P.点Q的坐
(a >0)与x轴的正半轴交于点P.点Q的坐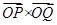 =6.
=6.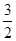 的直线交椭圆C于A、B两点,求△AOB的面积
的直线交椭圆C于A、B两点,求△AOB的面积 ,焦点是
,焦点是 ,点
,点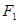 到直线
到直线 的距离为
的距离为 ,过点
,过点 且倾斜角为锐角的直线
且倾斜角为锐角的直线 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得 .
. 的距离为
的距离为 可知-
可知- +
+ ,设出点A(x1,y1)、B(x2,y2).,借助于向量公式
,设出点A(x1,y1)、B(x2,y2).,借助于向量公式 再利用 A、B在椭圆
再利用 A、B在椭圆 +y2=1上, 得到坐标的值,然后求解得到直线方程。
+y2=1上, 得到坐标的值,然后求解得到直线方程。

 ……10分
……10分 =
= .
. =0.
=0.