题目内容
如果函数y=2tan(2x+φ)的图象关于点( π,0)对称,则|φ|的最小值为( )
π,0)对称,则|φ|的最小值为( )A.

B.

C.

D.0
【答案】分析:正切函数y=tanx的对称中心为(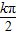 ,0),k∈Z,由已知可得
,0),k∈Z,由已知可得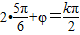 ,解得φ=
,解得φ=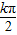 -
-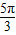 ,代入k的值验证即可.
,代入k的值验证即可.
解答:解:∵正切函数y=tanx的对称中心为(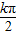 ,0),k∈Z,
,0),k∈Z,
∵函数y=2tan(2x+φ)的图象关于点( π,0)对称,
π,0)对称,
∴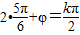 ,解得φ=
,解得φ=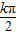 -
-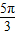 ,
,
当k=3时,φ=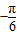 ,当k=4时,φ=
,当k=4时,φ=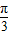 ,
,
故|φ|的最小值为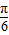 ,
,
故选C
点评:本题考查函数y=Atan(ωx+φ)的图象,易错点在于正切函数y=tanx的对称中心为(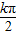 ,0),k∈Z,属中档题.
,0),k∈Z,属中档题.
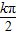 ,0),k∈Z,由已知可得
,0),k∈Z,由已知可得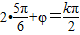 ,解得φ=
,解得φ=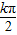 -
-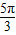 ,代入k的值验证即可.
,代入k的值验证即可.解答:解:∵正切函数y=tanx的对称中心为(
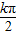 ,0),k∈Z,
,0),k∈Z,∵函数y=2tan(2x+φ)的图象关于点(
 π,0)对称,
π,0)对称,∴
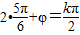 ,解得φ=
,解得φ=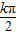 -
-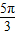 ,
,当k=3时,φ=
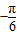 ,当k=4时,φ=
,当k=4时,φ=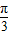 ,
,故|φ|的最小值为
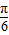 ,
,故选C
点评:本题考查函数y=Atan(ωx+φ)的图象,易错点在于正切函数y=tanx的对称中心为(
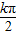 ,0),k∈Z,属中档题.
,0),k∈Z,属中档题. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 π,0)对称,则|φ|的最小值为( )
π,0)对称,则|φ|的最小值为( )

