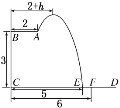
题目内容
【题目】如图，某小区准备将闲置的一直角三角形地块开发成公共绿地，图中
.设计时要求绿地部分（如图中阴影部分所示）有公共绿地走道
，且两边是两个关于走道对称的三角形（
和
）.现考虑方便和绿地最大化原则，要求点
与点
均不重合，
落在边
上且不与端点
重合，设
.
（1）若
，求此时公共绿地的面积；
（2）为方便小区居民的行走，设计时要求
的长度最短，求此时绿地公共走道的长度.
【答案】(1)
；(2)
.
【解析】分析：（1）由题意可得
，
，则
；
（2）由题意可得
，由正弦定理有
，记
，结合三角函数的性质可得
时，
取最大，
最短，则此时
.
详解：（1）由图得：
∴，
又
∴
∴，
∴
；
（2）由图得：
且
，
∴
，
在
中，由正弦定理可得:
，
∴
，
记
，
又
，∴
，
∴时，取最大，最短，则此时.
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
