题目内容
函数![]()
(I)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(II)设![]() ,若
,若![]() ,求证:对任意
,求证:对任意![]() ,且
,且![]() ,都有
,都有![]() .
.
解:(1)当![]() 时,
时,![]()
函数定义域为(![]() )且
)且
令![]() ,解得
,解得![]() 或
或![]() …………………2分
…………………2分
当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| + | 0 | _ | 0 | + |
|
| 增函数 | 极大值 | 减函数 | 极小值 | 增函数 |
………………4分
所以当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ; ……………………6分
; ……………………6分
(2)因为![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() (当且仅当
(当且仅当![]() 时等号成立),
时等号成立),
所以![]() 在区间
在区间![]() 上是增函数, ……………………10分
上是增函数, ……………………10分
从而对任意![]() ,当
,当![]() 时,
时,![]() ,
,
即![]() ,所以
,所以![]() . …………12分
. …………12分

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目

 时,求不等式
时,求不等式 的解集;
的解集; 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.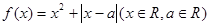 .
.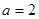 时,求
时,求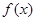 的单调区间;
的单调区间;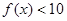 对
对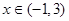 恒成立,求实数
恒成立,求实数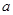 的取值范围.
的取值范围.
 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 时,讨论
时,讨论 的单调性.
的单调性. 
 时,求函数
时,求函数 的单调区间;
的单调区间; ;
; 若
若 的前n项和,求证:
的前n项和,求证: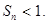

 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 时,讨论
时,讨论 的单调性.
的单调性.