Question

8．作出函数y=x${\;}^{\frac{6}{5}}$的图象，并根据图象比较（-$\frac{2}{3}$）${\;}^{\frac{6}{5}}$与（$\frac{3}{4}$）${\;}^{\frac{6}{5}}$的大小．

Answer 1

分析 根据幂函数的图象和性质，可得函数y=x${\;}^{\frac{6}{5}}$的图象，结合图象分析函数的奇偶性和单调性，要得（-$\frac{2}{3}$）${\;}^{\frac{6}{5}}$与（$\frac{3}{4}$）${\;}^{\frac{6}{5}}$的大小．

解答 解：函数y=x${\;}^{\frac{6}{5}}$的图象如图所示：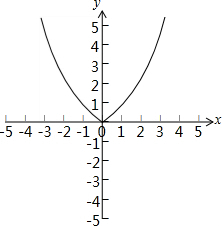

由图可得：函数为偶函数，且在（0，+∞）上为增函数，
故（-$\frac{2}{3}$）${\;}^{\frac{6}{5}}$=（$\frac{2}{3}$）${\;}^{\frac{6}{5}}$＜（$\frac{3}{4}$）${\;}^{\frac{6}{5}}$．

点评 本题考查的知识点是幂函数的图象和性质，熟练掌握幂函数的图象和性质，是解答的关键．