题目内容
已知b,c∈R,若关于的不等式0≤
+bx+c≤4的解集为[x1,x2]∪[x3,x4],(x2<x3),则(x2+x4)-(x1+x3)的取值范围为 .
| x | 2 |
分析:先画出函数f(x)=x2+bx+c的图象,数形结合可知x2、x3为方程 x2+bx+c=0的两个根,x1、x4为方程 x2+bx+c=4的两个根,利用求根公式将所求表示为关于
的函数,最后利用换元法求取值范围即可.
| b2-4c |
解答:解:依题意:x2、x3为方程x2+bx+c=0的两个根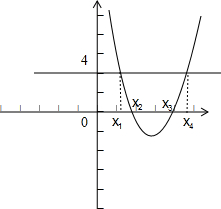 ,
,
x1、x4为方程x2+bx+c-4=0的两个根.
设y=(x2+x4)-(x1+x3)=(x4-x3)+(x2-x1)=2(x2-x1)
=2(
-
)
=2
.
令
=t,则t>0,
则y=
-t,(y>0)
∴(y+t)2=t2+16,
即2yt+y2=16,
t=
>0,解得4>y>0(或y<-4,不合题意,舍去),
故答案为:(0,4)
 ,
,x1、x4为方程x2+bx+c-4=0的两个根.
设y=(x2+x4)-(x1+x3)=(x4-x3)+(x2-x1)=2(x2-x1)
=2(
-b-
| ||
| 2 |
-b-
| ||
| 2 |
=2
| ||||
| 2 |
令
| b2-4c |
则y=
| t2+16 |
∴(y+t)2=t2+16,
即2yt+y2=16,
t=
| 16-y2 |
| 2y |
故答案为:(0,4)
点评:本题主要考查了函数、方程不等式间的内在联系及其相互应用,一元二次方程的解法,一元二次不等式的解法,换元法、求函数值域的方法,难度较大.

练习册系列答案
相关题目
 .
. 的方程
的方程 只有一个实数解,求实数
只有一个实数解,求实数 的取值范围;
的取值范围; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 R,若关于的不等式
R,若关于的不等式 的解集为
的解集为 的最小值是 .
的最小值是 .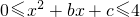 的解集为[x1,x2]∪[x3,x4],(x2<x3),则(2x4-x3)-(2x1-x2)的最小值是________.
的解集为[x1,x2]∪[x3,x4],(x2<x3),则(2x4-x3)-(2x1-x2)的最小值是________.