题目内容
如图△ABC中,BC=2(1)建立适当的坐标系,求双曲线D的方程;
(2)设过点E(1,0)的直线l分别与双曲线D的左、右支交于F、G点,直线l的斜率为K,求k的取值范围.
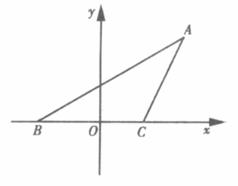
解:(1)以BC中点为原点,BC所在直线为z轴,建立坐标系.

则B(-![]() ,0),C(
,0),C(![]() ,0),设A(x0,y0)
,0),设A(x0,y0)
故![]() =(-
=(-![]() -x0,-y0),
-x0,-y0),
![]() =(
=(![]() -x0,-y0),
-x0,-y0),![]() =(-2
=(-2![]() ,0)
,0)
由 得
得 ∴
∴
设双曲线方程![]() =1(a>0,b>0),又c=
=1(a>0,b>0),又c=![]()
∴ ∴
∴
∴双曲线D的方程为![]() =1
=1
(2)当l⊥x轴时,l与双曲线无交点.
当l不垂直x轴时,可设l的方程:y=k(x-1)
由 消去y得
消去y得
(1-2k2)x2+4k2x-(2k2+2)=0
∵与双曲线左、右支交于F(x1,y1),G(x1,y2)
则 ∴
∴![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图△ABC中,AC=BC=
如图△ABC中,AC=BC=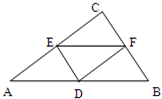 如图△ABC中,D,E,F分别是AB,AC,BC的中点,则下列各式不正确的是( )
如图△ABC中,D,E,F分别是AB,AC,BC的中点,则下列各式不正确的是( )
