题目内容
设函数f(x)=(Ⅰ)求证:0≤![]() <1;
<1;
(Ⅱ)若函数f(x)的递增区间为[s,t],求|s-t|的取值范围;
(Ⅲ)若当x≥k时(k是与a,b,c无关的常数),恒有f′(x)+a<0,试求k的最小值.
(Ⅰ)证明:f′(x)= ax2+2bx+c,由题意及导数的几何意义得
f′(1)=a+2b+c=0,(1)
f′(m)=am2+2bm+c=-a,(2)
又a<b<c,可得4a<a+2b+c<4c,
即4a<0<4c,故a<0,c>0,
由(1)得c=-a-2b,代入a<b<c,再由a<0,得![]() <1,(3)
<1,(3)
将c=-a-2b代入(2)得am2+2bm-2b=0,
即方程ax2+2bx-2b=0有实根.
故其差别式△=4b2+8ab≥0得
![]() ≤-2,或
≤-2,或![]() ≥0,(4)
≥0,(4)
由(3),(4)得0≤![]() <1;
<1;
(Ⅱ)解:由f′(x)= ax2+2bx+c的判别式
△′=4b2-4ac>0,
知方程f′(x)= ax2+2bx+c=0 (*)有两个不等实根,设为x1,x2,
又由f′(1)=a+2b+c=0知,x1=1为方程(*)的一个实根,则
由根与系数的关系得x1+x2=![]() ,x2=
,x2=![]() -1<0<x1,
-1<0<x1,
当x<x2或x>x1时,f′(x)<0,
当x2<x<x1时,f′(x)>0,
故函数f(x)的递增区间为[x2,x1],
由题设知[x2,x1]=[s,t],
因此|s-t|=| x1-x2|=2+![]() ,由(1)知0≤
,由(1)知0≤![]() <1得
<1得
|s-t|的取值范围为[2,4);
(Ⅲ)解:由f′(x)+a<0,即ax2+2bx+a+c<0,
即ax2+2bx-2b<0,
因为a<0,则x2+2·![]() x-2·
x-2·![]() >0,
>0,
整理得(2x-2)![]() +x2>0,
+x2>0,
设g(![]() )=(2x-2)
)=(2x-2)![]() +x2,可以看作是关于
+x2,可以看作是关于![]() 的一次函数,
的一次函数,
由题意g(![]() )>0对于0≤
)>0对于0≤![]() <1恒成立,
<1恒成立,
故![]() 即
即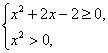
得x≤![]() -1或x≥
-1或x≥![]() -1,
-1,
由题意,[k,+∞)![]() (-∞ ,
(-∞ , ![]() -1]∪[
-1]∪[![]() -1,+∞),
-1,+∞),
故k≥![]() -1,因此A的最小值为
-1,因此A的最小值为![]() -1.
-1.
