题目内容
已知函数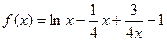 .
.
(Ⅰ)求函数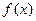 的单调区间;
的单调区间;
(Ⅱ)设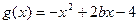 ,若对任意
,若对任意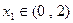 ,
,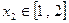 ,不等式
,不等式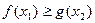 恒成立,求实数
恒成立,求实数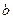 的取值范围
的取值范围
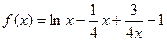 .
.(Ⅰ)求函数
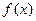 的单调区间;
的单调区间;(Ⅱ)设
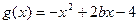 ,若对任意
,若对任意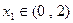 ,
,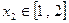 ,不等式
,不等式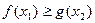 恒成立,求实数
恒成立,求实数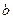 的取值范围
的取值范围解: (1)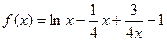
 ,
,
 ...................2分
...................2分
由 及
及 得
得 ;由
;由 及
及 得
得 ,
,
故函数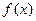 的单调递增区间是
的单调递增区间是 ;
;
单调递减区间是 。...................4分
。...................4分
(2)若对任意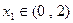 ,
,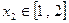 ,不等式
,不等式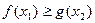 恒成立,
恒成立,
问题等价于 ,...................5分
,...................5分
由(1)可知,在 上,
上, 是函数极小值点,这个极小值是唯一的极值点,故也是最小值点,所以
是函数极小值点,这个极小值是唯一的极值点,故也是最小值点,所以 ;...................6分
;...................6分

当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;...................8分
;...................8分
问题等价于 或
或 或
或 ...............11分
...............11分
解得 或
或 或
或 
即 ,所以实数
,所以实数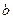 的取值范围是
的取值范围是
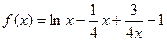
 ,
, ...................2分
...................2分由
 及
及 得
得 ;由
;由 及
及 得
得 ,
,故函数
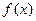 的单调递增区间是
的单调递增区间是 ;
;单调递减区间是
 。...................4分
。...................4分(2)若对任意
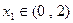 ,
,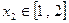 ,不等式
,不等式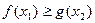 恒成立,
恒成立,问题等价于
 ,...................5分
,...................5分由(1)可知,在
 上,
上, 是函数极小值点,这个极小值是唯一的极值点,故也是最小值点,所以
是函数极小值点,这个极小值是唯一的极值点,故也是最小值点,所以 ;...................6分
;...................6分
当
 时,
时, ;
;当
 时,
时, ;
;当
 时,
时, ;...................8分
;...................8分问题等价于
 或
或 或
或 ...............11分
...............11分解得
 或
或 或
或 
即
 ,所以实数
,所以实数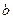 的取值范围是
的取值范围是
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
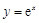 的图象在点
的图象在点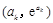 处的切线与
处的切线与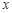 轴的交点的横坐标为
轴的交点的横坐标为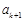 ,其中
,其中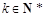 ,
,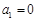 ,则
,则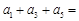
 知二次函数
知二次函数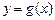 的图象经过点
的图象经过点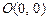 、
、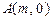 与点
与点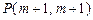 ,设函数
,设函数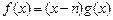 在
在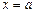 和
和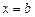 处取到极值,其中
处取到极值,其中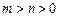 ,
,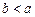 。
。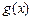 的二次项系数
的二次项系数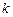 的值;
的值;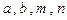 的大小(要求按从小到大排列);
的大小(要求按从小到大排列);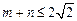 ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线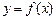 均相切,求
均相切,求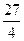 x2(1-x).
x2(1-x).  ;
; (x∈[0,+∞
(x∈[0,+∞ ,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由 则( )
则( )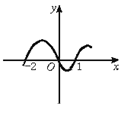
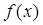 是偶函数,当
是偶函数,当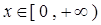 时,
时,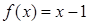 ,则
,则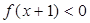 解集为:
解集为: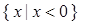



 在
在 内有定义,对于给定的正数
内有定义,对于给定的正数 ,定义函数:
,定义函数: ,取函数
,取函数 .当
.当 时,函数
时,函数 在下列区间上单调递减的是
在下列区间上单调递减的是



 在闭区间[-3,0]上的最大值,最小值分别为M,m,则M+m=
在闭区间[-3,0]上的最大值,最小值分别为M,m,则M+m=  ,
, ,对于任意的
,对于任意的 ,存在
,存在 使方程
使方程 成立,则
成立,则


