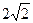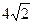题目内容
(本小题满分13分)
设椭圆 过点
过点 ,且着焦点为
,且着焦点为
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)当过点 的动直线
的动直线 与椭圆
与椭圆 相交与两不同点
相交与两不同点 时,在线段
时,在线段 上取点
上取点 ,满足
,满足 ,证明:点
,证明:点 总在某定直线上
总在某定直线上
设椭圆
 过点
过点 ,且着焦点为
,且着焦点为
(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)当过点
 的动直线
的动直线 与椭圆
与椭圆 相交与两不同点
相交与两不同点 时,在线段
时,在线段 上取点
上取点 ,满足
,满足 ,证明:点
,证明:点 总在某定直线上
总在某定直线上(Ⅰ)

(Ⅱ)见解析
(1)由题意:
 ,解得
,解得 ,所求椭圆方程为
,所求椭圆方程为
(2)方法一
设点Q、A、B的坐标分别为
 。
。由题设知
 均不为零,记
均不为零,记 ,则
,则 且
且
又A,P,B,Q四点共线,从而

于是
 ,
, 
 ,
, 
从而
 ,
,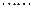 (1)
(1)  ,
,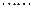 (2)
(2)又点A、B在椭圆C上,即


(1)+(2)×2并结合(3),(4)得

即点
 总在定直线
总在定直线 上
上方法二
设点
 ,由题设,
,由题设, 均不为零。
均不为零。且
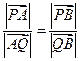
又
 四点共线,可设
四点共线,可设 ,于是
,于是 (1)
(1) (2)
(2)由于
 在椭圆C上,将(1),(2)分别代入C的方程
在椭圆C上,将(1),(2)分别代入C的方程 整理得
整理得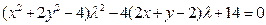 (3)
(3)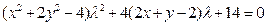 (4)
(4)(4)-(3) 得


即点
 总在定直线
总在定直线 上
上
练习册系列答案
相关题目
 的左焦点到直线
的左焦点到直线 的距离为
的距离为 ,求椭圆的方程。
,求椭圆的方程。 的直角顶点
的直角顶点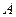 为动点,
为动点,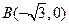 ,
,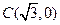 为两个定点,作
为两个定点,作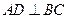 于
于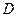 ,动点
,动点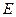 满足
满足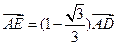 ,当点
,当点 ,曲线
,曲线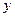 轴正半轴的交点为
轴正半轴的交点为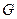 .(Ⅰ) 求曲线
.(Ⅰ) 求曲线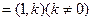 的直线
的直线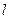 ,与曲线
,与曲线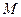 ,
,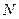 两点,使
两点,使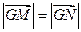 ,且
,且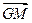 与
与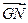 的夹角为
的夹角为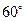 ?若存在,求出所有满足条件的直线方程;若不存在,说明理由.
?若存在,求出所有满足条件的直线方程;若不存在,说明理由.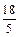 的距离之比是
的距离之比是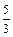 ,则点P的轨迹方程是( )
,则点P的轨迹方程是( )

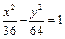

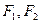 是椭圆
是椭圆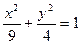 的两个焦点,
的两个焦点,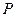 是椭圆上的点,且
是椭圆上的点,且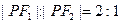 ,则
,则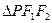 的面积为( )
的面积为( )