题目内容
已知函数 在一个周期内的图象如图所示
在一个周期内的图象如图所示(1)求函数f(x)的解析式;
(2)设
 ,求,
,求, 的值.
的值.
【答案】分析:(1)由图可知A,由其周期可求ω,利用- ω+φ=0可求φ;
ω+φ=0可求φ;
(2)由(1)可知函数f(x)的解析式,从而可求得g(x)= f(2x)•cosx的解析式,从而可得g(
f(2x)•cosx的解析式,从而可得g( )的值.
)的值.
解答:解:(1)由图知,A=2,T=4π,由T= =4π得,ω=
=4π得,ω= ;
;
又f(x)=2sin( x+φ)过(-
x+φ)过(- ,0),
,0),
∴- ω+φ=2kπ,k∈Z,又|φ|<
ω+φ=2kπ,k∈Z,又|φ|< ,
,
∴φ= .
.
∴f(x)=2sin( x+
x+ )
)
(2)∵g(x)= f(2x)•cosx=
f(2x)•cosx= ×2sin(x+
×2sin(x+ )cosx=sin(x+
)cosx=sin(x+ )cosx,
)cosx,
∴g( )=sin
)=sin •cos
•cos =-1×(-
=-1×(- )=
)= .
.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查运用诱导公式化简求值,属于中档题.
 ω+φ=0可求φ;
ω+φ=0可求φ;(2)由(1)可知函数f(x)的解析式,从而可求得g(x)=
 f(2x)•cosx的解析式,从而可得g(
f(2x)•cosx的解析式,从而可得g( )的值.
)的值.解答:解:(1)由图知,A=2,T=4π,由T=
 =4π得,ω=
=4π得,ω= ;
;又f(x)=2sin(
 x+φ)过(-
x+φ)过(- ,0),
,0),∴-
 ω+φ=2kπ,k∈Z,又|φ|<
ω+φ=2kπ,k∈Z,又|φ|< ,
,∴φ=
 .
.∴f(x)=2sin(
 x+
x+ )
)(2)∵g(x)=
 f(2x)•cosx=
f(2x)•cosx= ×2sin(x+
×2sin(x+ )cosx=sin(x+
)cosx=sin(x+ )cosx,
)cosx,∴g(
 )=sin
)=sin •cos
•cos =-1×(-
=-1×(- )=
)= .
.点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查运用诱导公式化简求值,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 在一个周期内的图象如下图所示。
在一个周期内的图象如下图所示。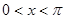 ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围和这两个根的和。
有两个不同的实数根,求实数m的取值范围和这两个根的和。
 在一个周期内的图象如图所示,则它的解析式为_
_。
在一个周期内的图象如图所示,则它的解析式为_
_。
 在一个周期内的图象如图所示,要得到函数
在一个周期内的图象如图所示,要得到函数 的图象,则需将函数
的图象,则需将函数 的图象( )
的图象( )

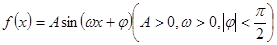 在一个周期内的部分函数图象如图所示.
在一个周期内的部分函数图象如图所示.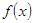 的解析式.
的解析式. 上的最大值和最小值.
上的最大值和最小值.
 在一个周期内的图象如下图所示.
在一个周期内的图象如下图所示.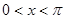 ,且方程
,且方程 有两个
有两个

 的取值范围.
的取值范围.