Question

【题目】设函数定义域为若在上单调递减,则称为函数的峰点, 为含峰函数.（特别地,若在上单调递增或递减,则峰点为1或0）.

对于不易直接求出峰点的含峰函数,可通过做试验的方法给出的近似值,试验原理为:“对任意的若则为含峰区间,此时称为近似峰点;若则为含峰区间,此时称为近似峰点”.

我们把近似峰点与之间可能出现的最大距离称为试验的“预计误差”,记为,其值为其中表示中较大的数

（Ⅰ）若求此试验的预计误差;

（Ⅱ）如何选取才能使这个试验方案的预计误差达到最小?并证明你的结论（只证明的取值即可）.

（Ⅲ）选取可以确定含峰区间为或在所得的含峰区间内选取,由与或与类似地可以进一步得到一个新的预计误差.分别求出当和时预计误差的最小值.（本问只写结果,不必证明）

Answer 1

【答案】(1) (2)见解析;(3)见解析.

【解析】试题分析： 由已知，求出时，此试验的预计误差取此时试验的预计误差为，再分两种情况讨论点的位置，从而证明这是使试验误差达到最小的试验设计当时预计误差的最小值为，当时预计误差的最小值为

解析：（Ⅰ）由已知得

所以

（Ⅱ）取此时试验的预计误差为

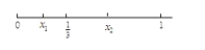证明:分两种情况讨论,

当时,如图所示,

如果那么

如果那么

当

综上,当时,

同理可得当时,

即时,试验的预计误差最小.

（Ⅲ）当和时预计误差的最小值分别为和