题目内容

平面直角坐标系xOy中，A（1，0），B（0，1），C（2，5），D是AC上的动点，满足
AD
=λ
AC
（λ∈R）．
（Ⅰ）求|2
AB
+
AC
|的值；
（Ⅱ）求cos∠BAC；
（Ⅲ）若
BD
⊥
BA
，求实数λ的值．
分析：（Ⅰ）由已知计算2
AB
+
AC
=(-1，7)，根据向量的数量积的性质可求
（Ⅱ）根据向量的夹角公式cos∠BAC=
AB
•
AC
|
AB
||
AC
|
可求
（Ⅲ）由
BD
⊥
BA
，可得
BD
•
BA
=0，从而可得关于λ的方程，求解即可
解答：解：（Ⅰ）因为
AB
=(-1，1)，
AC
=(1，5)，所以2
AB
+
AC
=(-1，7)（2分）
|2
AB
+
AC
|=
(-1)2+72
=5
2
（4分）
（Ⅱ）因为cos∠BAC=
AB
•
AC
|
AB
||
AC
|
（6分）
所以cos∠BAC=
(-1)×1+1×5
(-1)2+12
•
12+52
=
2
13
13
（9分）
（Ⅲ）
BD
=
AD
-
AB
=λ(1，5)-(-1，1)=(λ+1，  5λ-1)（11分）
因为
BD
⊥
BA
，所以
BD
•
BA
=0（13分）
BA
=(1，-1)即（λ+1）×1+（5λ-1）×（-1）=0，解得λ=
1
2
（14分）
点评：本题主要综合考查了向量的模的求解，向量的夹角公式的求解及向量垂直的坐标表示等向量的数量积的性质的运用．
练习册系列答案
相关题目
在平面直角坐标系xOy中，“方程
x2
k-1
+
y2
k-3
=1表示焦点在x轴上的双曲线”的充要条件是k∈
 
．
在平面直角坐标系xOy中，Pn（n，n2）（n∈N+）是抛物线y=x2上的点，△OPnPn+1的面积为Sn．
（1）求Sn；
（2）化简
1
S1
+
1
S2
+…+
1
Sn
；
（3）试证明S1+S2+…+Sn=
n(n+1)(n+2)
6
．
已知平面直角坐标系xOy中，A(4+2
3
，2)，B(4，4)，圆C是△OAB的外接圆．
（1）求圆C的方程；
（2）若过点（2，6）的直线l被圆C所截得的弦长为4
3
，求直线l的方程．
在平面直角坐标系xOy中，直线l的参数方程为：
x=-2+
3
5
t
y=2+
4
5
t
（t为参数），它与曲线C：（y-2）2-x2=1交于A，B两点．
（1）求|AB|的长；
（2）在以O为极点，x轴的正半轴为极轴建立极坐标系，设点P的极坐标为(2
2
，
3π
4
)，求点P到线段AB中点M的距离．
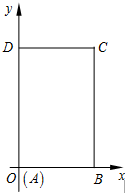精英家教网如图，在平面直角坐标系xOy中，已知矩形ABCD的两边AB，CD分别落在x轴、y轴的正半轴上，且AB=2，AD=4，点A与坐标原点重合．现将矩形折叠，使点A落在线段DC上，若折痕所在的直线的斜率为k，试写出折痕所在直线的方程及k的范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网