题目内容
(2013•唐山二模)函数f(x)=2sinπx-
所有零点的和等于( )
| 3x-x2 |
分析:依题意,令h(x)=2sinπx,g(x)=
(两函数的交点就是方程的解),逐段分析即可求得零点个数,利用h(x)=2sinπx与g(x)=
都关于x=
对称即可求得所有零点的和.
| 3x-x2 |
| 3x-x2 |
| 3 |
| 2 |
解答:解:依题意,0≤x≤3,函数f(x)=2sinπx-
的零点,即方程2sinπx=
的解.
令h(x)=2sinπx,则其周期T=2;
令y=g(x)=
,
则y2+(x-
)2=
(y≥0),其轨迹为以(
,0)为圆心,
为半径的上半圆;
∵h(x)=2sinπx与g(x)=
都关于x=
对称,那么只要判断解的个数就可以.
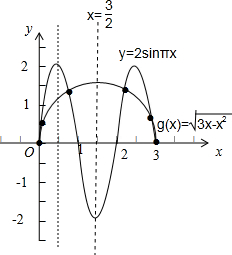
∵h(0)=g(0),两函数都从原点出发(0,0)是一个交点;
又h(
)=2>g(
)=
,f(
)=h(
)-g(
)>0;
h(1)=0,g(1)=
,f(1)=h(1)-g(1)<0,
∴h(x)=g(x)区间(0,
)内有1个交点,在区间(
,1)内有1个交点;
同理可知,h(x)=g(x)区间(2,2
)内有1个交点,在区间(2
,3)内有1个交点,在x=3处有1个交点;
由h(x)=2sinπx与g(x)=
都关于x=
对称得:6个交点的横坐标相加等于3×(2×
)=9.
所有零点的和是9.
故选C
| 3x-x2 |
| 3x-x2 |
令h(x)=2sinπx,则其周期T=2;
令y=g(x)=
| 3x-x2 |
则y2+(x-
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
∵h(x)=2sinπx与g(x)=
| 3x-x2 |
| 3 |
| 2 |
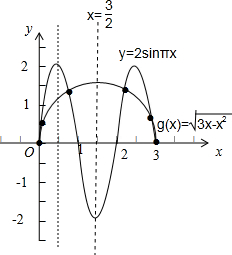
∵h(0)=g(0),两函数都从原点出发(0,0)是一个交点;
又h(
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
h(1)=0,g(1)=
| 2 |
∴h(x)=g(x)区间(0,
| 1 |
| 2 |
| 1 |
| 2 |
同理可知,h(x)=g(x)区间(2,2
| 1 |
| 2 |
| 1 |
| 2 |
由h(x)=2sinπx与g(x)=
| 3x-x2 |
| 3 |
| 2 |
| 3 |
| 2 |
所有零点的和是9.
故选C
点评:本题考查根的存在性及根的个数判断,考查函数的图象与性质,考查分析与运算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目