题目内容
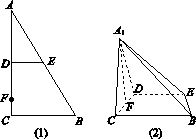
（2012•北京）如图，∠ACB=90°，CD⊥AB于点D，以BD为直径的圆与BC交于点E．则（ ）分析：连接DE，以BD为直径的圆与BC交于点E，DE⊥BE，由∠ACB=90°，CD⊥AB于点D，△ACD∽△CBD，由此利用三角形相似和切割线定理，能够推导出CE•CB=AD•BD．
解答：
解：连接DE，
∵以BD为直径的圆与BC交于点E，
∴DE⊥BE，
∵∠ACB=90°，CD⊥AB于点D，
∴△ACD∽△CBD，
∴
=
，
∴CD2=AD•BD．
∵CD2=CE•CB，
∴CE•CB=AD•BD，
故选A．
解：连接DE，∵以BD为直径的圆与BC交于点E，
∴DE⊥BE，
∵∠ACB=90°，CD⊥AB于点D，
∴△ACD∽△CBD，
∴
| CD |
| BD |
| AD |
| CD |
∴CD2=AD•BD．
∵CD2=CE•CB，
∴CE•CB=AD•BD，
故选A．
点评：本题考查与圆有关的比例线段的应用，是基础题．解题时要认真审题，仔细解答，注意三角形相似和切割线定理的灵活运用．
练习册系列答案
一线名师提优试卷系列答案
相关题目
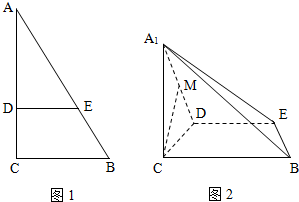（2012•北京）如图1，在Rt△ABC中，∠C=90°，BC=3，AC=6，D，E分别是AC，AB上的点，且DE∥BC，DE=2，将△ADE沿DE折起到△A1DE的位置，使A1C⊥CD，如图2．
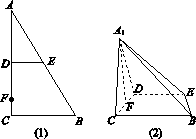
（2012•北京）如图1，在Rt△ABC中，∠C=90°，D，E分别为AC，AB的中点，点F为线段CD上的一点，将△ADE沿DE折起到△A1DE的位置，使A1F⊥CD，如图2．
