题目内容

已知
e1
，
e2
为一组基底，
a
=k
e1
+
e2
，
b
=
e1
+k
e2
，若
a
∥
b
，则k=
±1
±1
．
分析：由条件利用两个向量共线的性质可得 k2-1×1=0，由此求得k的值．
解答：解：由于
e1
，
e2
为一组基底，
a
=k
e1
+
e2
，
b
=
e1
+k
e2
，若
a
∥
b
，则有 k2-1×1=0，
解得k=±1，
故答案为±1．
点评：本题主要考查两个向量共线的性质，属于基础题．
练习册系列答案
相关题目
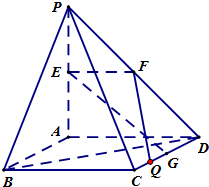精英家教网（理）如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，点E、F、G分别为线段PA、PD和CD的中点．
（1）求异面直线EG与BD所成角的大小；
（2）在线段CD上是否存在一点Q，使得点A到平面EFQ的距离恰为
4
5
？若存在，求出线段CQ的长；若不存在，请说明理由．
（文）已知坐标平面内的一组基向量为
e
1=(1，sinx)，
e
2=(0，cosx)，其中x∈[0，
π
2
)，且向量
a
=
1
2
e
1+
3
2
e
2．
（1）当
e
1和
e
2都为单位向量时，求|
a
|；
（2）若向量
a
和向量
b
=(1，2)共线，求向量
e
1和
e
2的夹角．
下列说法中，正确的个数为（　　）
（1）
AB
+
MB
+
BC
+
OM
+
CO
=
AB

（2）已知向量
a
=（6，2）与
b
=（-3，k）的夹角是钝角，则k的取值范围是k＜0
（3）若向量
e1
=(2，-3)，
e2
=(
1
2
，-
3
4
)能作为平面内所有向量的一组基底
（4）若
a
∥
b
，则
a
在
b
上的投影为|
a
|．
（2011•洛阳二模）给出下列命题：
①设向量
e1
，
e2
满足|
e1
|=2，|
e2
|=1，
e1
，
e2
的夹角为
π
3
．若向量2t
e1
+7
e2
与
e1
+t
e2
的夹角为钝角，则实数t的取值范围是（-7，-
1
2
）；
②已知一组正数x1，x2，x3，x4的方差为s2=
1
4
（x12+x22+x32+x42）-4，则x1+1，x2+1，x3+1，x4+1的平均数为1
③设a，b，c分别为△ABC的角A，B，C的对边，则方程x2+2ax+b2=o与x2+2cx-b2=0有公共根的充要条件是A=90°；
④若f（n）表示n2+1（n∈N）的各位上的数字之和，如112+1=122，1+2+2=5，所以f（n）=5，记f1（n）=f（n），f2（n）=f[f1（n）]，…fk+1（n）=f[fk（n）]，k∈N，则f20（5）=11．
上面命题中，假命题的序号是
②
②
 （写出所有假命题的序号）．
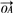已知{e1 ，e2 ，e3} 为空间一基底，且以=e1+2e2-e3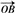，=-3e1+e2+2e3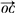，=e1+e2-e3，能否以作为空间的一组基底？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网