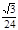题目内容
如图,PA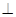 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB=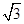 ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.
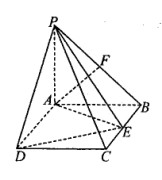
(I)求三棱锥E—PAD的体积;
(II)试问当点E在BC的何处时,有EF//平面PAC;
(1lI)证明:无论点E在边BC的何处,都有PE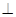 AF.
AF.
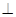 平面ABCD,四边形ABCD为矩形,PA=AB=
平面ABCD,四边形ABCD为矩形,PA=AB=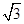 ,AD=1,点F是PB的中点,点E在边BC上移动.
,AD=1,点F是PB的中点,点E在边BC上移动.
(I)求三棱锥E—PAD的体积;
(II)试问当点E在BC的何处时,有EF//平面PAC;
(1lI)证明:无论点E在边BC的何处,都有PE
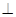 AF.
AF.见解析
试题分析:(Ⅰ)注意到PA
 平面ABCD,得知
平面ABCD,得知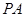 的长即为三棱锥
的长即为三棱锥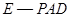 的高,而三棱锥
的高,而三棱锥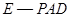 的体积等于
的体积等于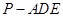 的体积,计算即得.
的体积,计算即得.(Ⅱ)当点
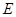 为
为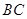 的中点时,
的中点时,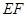 与平面
与平面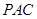 平行.
平行.利用三角形中位线定理,得到
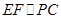 ,进一步得出
,进一步得出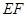 ∥平面
∥平面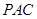 .
.(Ⅲ)证明:根据等腰三角形得出
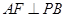 ,根据
,根据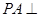 平面
平面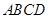 ,
,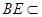 平面
平面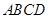 ,
,得到
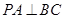 ,又因为
,又因为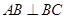 且
且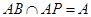 ,
,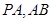 ?平面
?平面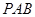 ,得到
,得到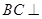 平面
平面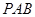 ,又
,又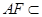 平面
平面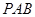 ,
,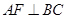 .
.再根据
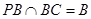 ,
,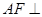 平面
平面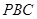 ,及
,及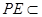 平面
平面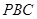 ,根据
,根据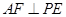 ,作出结论.
,作出结论.试题解析:(Ⅰ)由已知PA
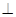 平面ABCD,所以
平面ABCD,所以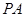 的长即为三棱锥
的长即为三棱锥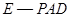 的高,三棱锥
的高,三棱锥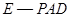 的体积等于
的体积等于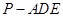 的体积
的体积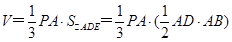
=
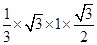 =
= 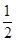 .
.(Ⅱ)当点
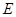 为
为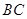 的中点时,
的中点时,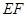 与平面
与平面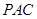 平行.
平行.∵在
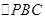 中,
中,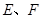 分别为
分别为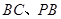 的中点,连结
的中点,连结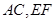
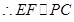 ,又
,又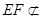 平面
平面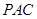 ,而
,而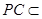 平面
平面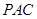 ,
,∴
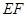 ∥平面
∥平面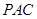 .
.(Ⅲ)证明:因为
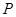
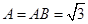 ,所以等腰三角形
,所以等腰三角形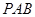 中,
中,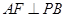
∵
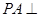 平面
平面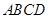 ,
,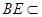 平面
平面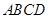 ,
,∴
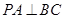
又因为
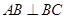 且
且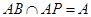 ,
,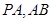 ?平面
?平面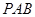 ,
,∴
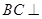 平面
平面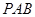 ,又
,又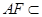 平面
平面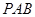 ,
,∴
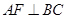 .
.又∵
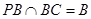 ,
,∴
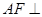 平面
平面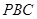 .PB,BE?平面PBE,
.PB,BE?平面PBE,∵
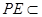 平面
平面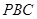 ,
,∴
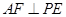 ,即无论点E在边
,即无论点E在边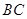 的何处,都有
的何处,都有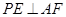 .
.
练习册系列答案
相关题目
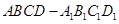 中,
中,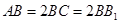 , 沿平面
, 沿平面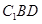 把这个长方体截成两个几何体: 几何体(1);几何体(2)
把这个长方体截成两个几何体: 几何体(1);几何体(2)
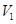 、
、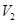 ,求
,求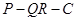 的正切值
的正切值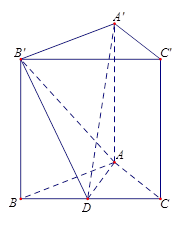
 B'D;
B'D; 的对角线交于点G,AD⊥平面
的对角线交于点G,AD⊥平面 ,
,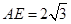 ,
,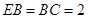 ,
,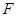 为
为 上的点,且BF⊥平面ACE
上的点,且BF⊥平面ACE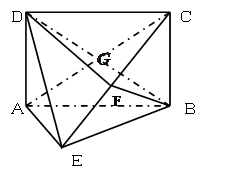
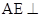 平面
平面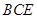 ;
;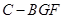 的体积.
的体积.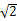 ,AA1=3,E为CD上一点,DE=1,EC=3
,AA1=3,E为CD上一点,DE=1,EC=3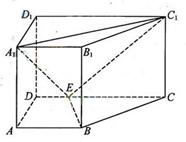
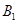 到平面EA1C1的距离.
到平面EA1C1的距离.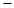 ABC中,E,F分别是AC,PC的中点,若EF
ABC中,E,F分别是AC,PC的中点,若EF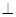 BF,AB=2,则三棱锥P
BF,AB=2,则三棱锥P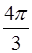 ,则圆锥的体积是________
,则圆锥的体积是________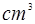 .
.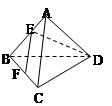
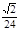 B.
B. 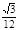 C.
C.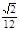 D.
D.