题目内容
过圆O:x2+y2=R2外一点A(a,b)引圆的两条切线AB和AC(其中B、C是切点),求经过这两个切点的直线l的方程.
解法一:连结OB、OC,则AB⊥OB,AC⊥OC,
∴B、C两点在以OA为直径的圆(x-a)x+(y-b)y=0上
∴x2+y2-ax-by=0①
由已知,⊙O的方程为x2+y2=R2②
②-①得ax+by=R2为所求直线l的方程.
解法二:设切点B、C的坐标分别为(x1,y1)、(x2,y2),则过B点的切线方程为x1x+y1y=R2;过C点的切线方程为x2x+y2y=R2;
又∵切线AB、AC交于A(a,b)点,即点A在两切线上,
∴![]()
这就是说,坐标(x1,y1)、(x2,y2)适合方程ax+by=R2.
∴方程ax+by=R2为直线l的方程.

练习册系列答案
相关题目
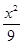 +
+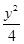 =1的交点个数为( )
=1的交点个数为( )