题目内容
直线L:x+2y-3=0与圆C:x2+y2+x-6y+m=0有两个交点A、B,O为坐标原点,若 ,则m的值是
,则m的值是
- A.2
- B.-1
- C.3
- D.

C
分析:由圆C与直线L的方程联立,消去x整理成关于y的一元二次方程,设出A(x1,y1)、B(x2,y2)两点坐标,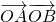 =x1•x2+y1•y2,由韦达定理可以求得答案.
=x1•x2+y1•y2,由韦达定理可以求得答案.
解答:由题意知,直线L:x+2y-3=0与圆C:x2+y2+x-6y+m=0,
由 ,消去x,得5y2-20y+12+m=0,
,消去x,得5y2-20y+12+m=0,
设A(x1,y1),B(x2,y2),
则 ,
,
x1•x2=(3-2y1)•(3-2y2)=4y1•y2-6(y1+y2)+9.
∴ =x1•x2+y1•y2=5y1•y2-6(y1+y2)+9=12+m-6×4+9=0,
=x1•x2+y1•y2=5y1•y2-6(y1+y2)+9=12+m-6×4+9=0,
解得m=3
故选C.
点评:本题考查圆的方程,以及直线与圆相交的性质,数量积判断两个平面向量的垂直关系,考查方程思想.属于基础题.
分析:由圆C与直线L的方程联立,消去x整理成关于y的一元二次方程,设出A(x1,y1)、B(x2,y2)两点坐标,
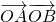 =x1•x2+y1•y2,由韦达定理可以求得答案.
=x1•x2+y1•y2,由韦达定理可以求得答案.解答:由题意知,直线L:x+2y-3=0与圆C:x2+y2+x-6y+m=0,
由
 ,消去x,得5y2-20y+12+m=0,
,消去x,得5y2-20y+12+m=0,设A(x1,y1),B(x2,y2),
则
 ,
,x1•x2=(3-2y1)•(3-2y2)=4y1•y2-6(y1+y2)+9.
∴
 =x1•x2+y1•y2=5y1•y2-6(y1+y2)+9=12+m-6×4+9=0,
=x1•x2+y1•y2=5y1•y2-6(y1+y2)+9=12+m-6×4+9=0,解得m=3
故选C.
点评:本题考查圆的方程,以及直线与圆相交的性质,数量积判断两个平面向量的垂直关系,考查方程思想.属于基础题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目