题目内容
16.已知$f(x)=\frac{ax+2}{{{x^2}+1}}$为R上的偶函数.(Ⅰ)求实数a的值;
(Ⅱ)判断函数f(x)在[0,+∞)上的单调性,并利用定义证明.
分析 (Ⅰ)由f(x)为R上的偶函数便可得到f(-1)=f(1),这样即可得出a=0;
(Ⅱ)可看出$f(x)=\frac{2}{{x}^{2}+2}$在[0,+∞)上单调递减,根据减函数的定义:设任意的x2>x1≥0,然后作差,通分,证明f(x2)<f(x1)便可得出f(x)在[0,+∞)上单调递减.
解答 解:(Ⅰ)∵f(x)为R上的偶函数;
∴f(-1)=f(1);
∴$\frac{-a+2}{1+1}=\frac{a+2}{1+1}$;
∴a=0;
(Ⅱ)函数$f(x)=\frac{2}{{{x^2}+1}}$在[0,+∞)上单调递减;
证明:设x2>x1≥0,则:
$f({x_2})-f({x_1})=\frac{2}{x_2^2+1}-\frac{2}{x_1^2+1}$
=$\frac{2(x_1^2-x_2^2)}{(x_2^2+1)(x_1^2+1)}$
=$\frac{{2({x_1}-{x_2})({x_1}+{x_2})}}{(x_2^2+1)(x_1^2+1)}$;
∵x2>x1≥0;
∴x1-x2<0,x1+x2>0,$x_1^2+1>0$,$x_2^2+1>0$;
∴$\frac{{2({x_1}-{x_2})({x_1}+{x_2})}}{(x_2^2+1)(x_1^2+1)}<0$;
即f(x2)-f(x1)<0;
∴f(x2)<f(x1);
∴函数f(x)在[0,+∞)上是单调递减函数.
点评 考查偶函数的定义,减函数的定义,以及根据减函数的定义判断和证明一个函数为减函数的方法和过程,作差的方法比较f(x1),f(x2),作差后是分式的一般要通分,以及平方差公式.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
7.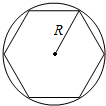 如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )
如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )
 如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )
如图,半径为R的圆形纸板上有一内接正六边形图案,将一颗豆子随机地扔到平放的纸板上,假设豆子不落在线上,则豆子落在正六边形区域的概率是( )| A. | $\frac{3}{2π}$ | B. | $\frac{3\sqrt{3}}{2π}$ | C. | $\frac{3}{4π}$ | D. | $\frac{3\sqrt{3}}{4π}$ |
4.“m=1”是“直线(m-2)x-3my-1=0与直线(m+2)x+(m-2)y+3=0相互垂直”的( )
| A. | 必要而不充分条件 | B. | 充分而不必要条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
11.某市刑警队对警员进行技能测试,测试成绩分为优秀、良好、合格三个等级,测试结果如下表:(单位:人)
若按优秀、良好、合格三个等级分层,从中抽取40人,成绩为良好的有24人,则a等于( )
| 优秀 | 良好 | 合格 | |
| 男 | 40 | 105 | 25 |
| 女 | a | 15 | 5 |
| A. | 10 | B. | 15 | C. | 20 | D. | 30 |
1.已知数列{an}满足:${a_1}=1,{a_{n+1}}=\frac{a_n}{{{a_n}+2}}(n∈N*)$,${C_n}=(1+\frac{1}{a_n})(\frac{2}{n+1}-λ)$,若{Cn}是单调递减数列,则实数λ的取值范围是( )
| A. | λ$≥\frac{1}{3}$ | B. | λ$>\frac{1}{3}$ | C. | λ$≥\frac{4}{3}$ | D. | λ$>\frac{4}{3}$ |
8.若p∨q为真命题,则下列结论不可能成立的是( )
| A. | p真q真 | B. | p假q真 | C. | p真q假 | D. | p假q假 |
6.已知满足条件x2+y2≤1的点(x,y)构成的平面区域的面积为S1,满足条件[x2]+[y]2≤1的点(x,y)构成的平面区域的面积为S2,(其中[x]、[y]分别表示不大于x、y的最大整数),则点(S1,S2)一定在( )
| A. | 直线x-y=0上 | B. | 直线2x-y-1=0右下方的区域内 | ||
| C. | 直线x+y-8=0左下方的区域内 | D. | 直线x-y+2=0左上方的区域内 |