题目内容

（2011•丹东模拟）函数y=log2(4x+1)-x的值域是（　　）
分析：先根据对数的运算性质进行化简，然后利用基本不等式求出对数的真数的取值范围，从而求出该函数的值域．
解答：解：y=log2(4x+1)-x=log2
4x+1
2x
=log2(2x+
1
2x
)
∵2x+
1
2x
≥2
2x•
1
2x
=2当x=0时取等号
∴y=log2(2x+
1
2x
)≥log22=1
∴函数y=log2(4x+1)-x的值域是[1，+∞）
故选C．
点评：本题主要考查了对数函数的值域，以及利用基本不等式求值域，同时考查了计算能力，属于基础题．
练习册系列答案
相关题目
（2011•丹东模拟）设l、m是两条不同的直线，α、β是两个不同的平面，给出下列5个命题：
①若m⊥α，l⊥β，则l∥α；
②若m⊥α，l?β，l∥m，则α⊥β；
③若α∥β，l⊥α，m∥β，则l⊥m；
④若α∥β，l∥α，m?β，则l∥m；
⑤若α⊥β，α∩β=l，m⊥l，则m⊥β．
其中正确命题的个数是（　　）
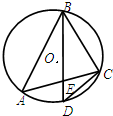（2011•丹东模拟）选修4-1：几何证明选讲
如图，⊙O是△ABC的外接圆，D是的中点，BD交AC于E．
（Ⅰ）求证：CD2=DE•DB；
（Ⅱ）若CD=2
3
，O到AC的距离为1，求⊙O的半径r．
（2011•丹东模拟）选修4-5：不等式选讲
设正有理数x是
3
的一个近似值，令y=1+
2
1+x
．
（Ⅰ）若x＞
3
，求证：y＜
3
；
（Ⅱ）求证：y比x更接近于
3
．
（2011•丹东模拟）已知椭圆C：
y2
a2
+
x2
b2
=1（a＞b＞0）经过点（
1
2
，
3
），一个焦点是F（0，-
3
）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设椭圆C与y轴的两个交点为A1、A2，点P在直线y=a2上，直线PA1、PA2分别与椭圆C交于M、N两点．试问：当点P在直线y=a2上运动时，直线MN是否恒经过定点Q？证明你的结论．
（2011•丹东模拟）已知实数x、y足约束条件
x-y+2≥0
x+y-4≥0
2x-y-5≤0
，若使得目标函数ax+y取最大值时有唯一最优解（1，3），则实数a的取值范围是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网