题目内容
已知函数f(n)=
,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014= .
|
考点:棱柱、棱锥、棱台的体积
专题:函数的性质及应用,等差数列与等比数列
分析:分类讨论得出n为奇数时 n+1为偶数;n为偶数,n+1为奇数.当n为奇数时,an=n2-(n+1)2=-2n-1,当n为偶数时,an=-n2+(n+1)2=2n+1,
运用列举法求出部分项,确定规律即可求解答案.
运用列举法求出部分项,确定规律即可求解答案.
解答:
解:n为奇数时 n+1为偶数;n为偶数,n+1为奇数.
当n为奇数时,an=n2-(n+1)2=-2n-1,
当n为偶数时,an=-n2+(n+1)2=2n+1
∴a1=-3,a2=5,a3=-7,a4=9,a5=-11,a6=13m,…,
∴a1+a2=2,a3+a4=2,
即a1+a2+a3+…+a2014=2×1007=2014,
故答案为:2014.
当n为奇数时,an=n2-(n+1)2=-2n-1,
当n为偶数时,an=-n2+(n+1)2=2n+1
∴a1=-3,a2=5,a3=-7,a4=9,a5=-11,a6=13m,…,
∴a1+a2=2,a3+a4=2,
即a1+a2+a3+…+a2014=2×1007=2014,
故答案为:2014.
点评:本题考查了数列的函数性质,运用整体求解,分类讨论得出函数值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
以边长为1的正方形的一条边为旋转轴,旋转一周后所得旋转体侧面积为( )
| A、2π | B、π | C、2 | D、1 |
设F1,F2分别为双曲线
-
=1(a>0,b>0)的左、右焦点,若在右支上存在点A,使得点F2到直线AF1的距离为2a,则该双曲线的离心率的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
B、(
| ||
| C、(1,2) | ||
| D、(2,+∞) |
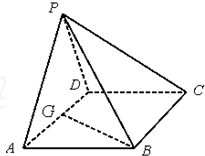 如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是∠DAB=60°且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD,G为AD的中点.