题目内容
下列方程所表示的直线能与抛物线 与曲线y2-x2=1(y≤-1)都相切的是
与曲线y2-x2=1(y≤-1)都相切的是
- A.

- B.

- C.

- D.

C
分析:假设直线方程,分别与抛物线 、曲线y2-x2=1(y≤-1)联立,利用判别式,代入验证,即可求得结论.
、曲线y2-x2=1(y≤-1)联立,利用判别式,代入验证,即可求得结论.
解答:设切线方程为y=kx+b,代入抛物线方程可得 ,∴△1=
,∴△1= ,∴
,∴
y=kx+b,代入曲线y2-x2=1(y≤-1)可得(k2-1)x2+2kx+b2-1=0,∴△2=4k2-4(k2-1)(b2-1)=0
代入验证,对于A,k=1,b=- ,此时△1=0,△2≠0;
,此时△1=0,△2≠0;
对于B,k=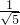 ,b=-
,b=- ,此时△1=0,△2≠0;
,此时△1=0,△2≠0;
对于C,k= ,b=-
,b=-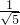 ,此时△1=0,△2=0;
,此时△1=0,△2=0;
对于D,k=2,b=- ,此时△1=0,△2≠0;
,此时△1=0,△2≠0;
故选C.
点评:本题考查直线与曲线的位置关系,考查学生的计算能力,属于中档题.
分析:假设直线方程,分别与抛物线
 、曲线y2-x2=1(y≤-1)联立,利用判别式,代入验证,即可求得结论.
、曲线y2-x2=1(y≤-1)联立,利用判别式,代入验证,即可求得结论.解答:设切线方程为y=kx+b,代入抛物线方程可得
 ,∴△1=
,∴△1= ,∴
,∴
y=kx+b,代入曲线y2-x2=1(y≤-1)可得(k2-1)x2+2kx+b2-1=0,∴△2=4k2-4(k2-1)(b2-1)=0
代入验证,对于A,k=1,b=-
 ,此时△1=0,△2≠0;
,此时△1=0,△2≠0;对于B,k=
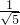 ,b=-
,b=- ,此时△1=0,△2≠0;
,此时△1=0,△2≠0;对于C,k=
 ,b=-
,b=-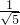 ,此时△1=0,△2=0;
,此时△1=0,△2=0;对于D,k=2,b=-
 ,此时△1=0,△2≠0;
,此时△1=0,△2≠0;故选C.
点评:本题考查直线与曲线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 ,则xy=96;
,则xy=96;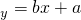 所表示的直线必恒经过点(1.5,2);
所表示的直线必恒经过点(1.5,2); ”的概率为
”的概率为 .
. ,则xy=96;
,则xy=96; 所表示的直线必恒经过点(1.5,2);
所表示的直线必恒经过点(1.5,2); ”的概率为
”的概率为 .
. 与曲线y2-x2=1(y≤-1)都相切的是( )
与曲线y2-x2=1(y≤-1)都相切的是( )


