题目内容
如图,已知正方形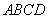 的边长为
的边长为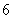 ,点
,点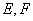 分别在边
分别在边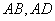 上,
上,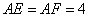 ,现将△
,现将△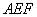 沿线段
沿线段 折起到△
折起到△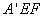 位置,使得
位置,使得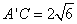 .
.
(1)求五棱锥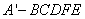 的体积;
的体积;
(2)求平面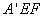 与平面
与平面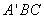 的夹角.
的夹角.
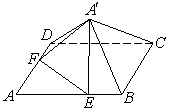 |
解(1)连接 ,设
,设 ,由
,由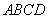 是正方形,
是正方形,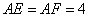 ,
,
得 是
是 的中点,且
的中点,且 ,从而有
,从而有 ,
,
所以 平面
平面 ,从而平面
,从而平面
 平面
平面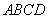 ,
,
 过点
过点 作
作 垂直
垂直 且与
且与 相交于点
相交于点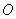 ,
,
则 平面
平面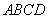 因为正方形
因为正方形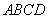 的边长为
的边长为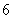 ,
,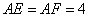 ,
,
得到: ,
,
所以 ,
,
所以
所以五棱锥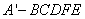 的体积
的体积
(2)由(1)知道
 平面
平面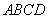 ,且
,且 ,即点
,即点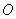 是
是 的交点,
的交点,
 如图以点
如图以点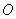 为原点,
为原点, 所在直线分别为
所在直线分别为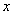 轴,
轴, 轴,
轴, 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则 ,
,
设平面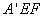 的法向量为
的法向量为 ,则
,则
 ,
,
 ,
,
令 ,则
,则 ,
,
设平面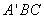 的法向量
的法向量 ,则
,则 ,
,

 ,
,
令 ,则
,则 ,即
,即 ,
,
所以 ,即平面
,即平面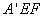 与平面
与平面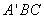 夹角
夹角 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
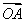 ·
·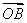 的值;
的值; C.
C. D.
D.

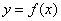 是周期为2的周期函数,且当
是周期为2的周期函数,且当 时,
时, ,则函数
,则函数 的零点个数是
的零点个数是 ,其中
,其中 ,则
,则 =( ).
=( ). ,
, 是双曲线
是双曲线 :
: 与椭圆
与椭圆 的公共焦点,点
的公共焦点,点 是
是 ,
, 在第一象限的公共点.若|F1F2|=|F1A|,则
在第一象限的公共点.若|F1F2|=|F1A|,则

 B.
B. C.
C. D.
D.
 的导函数为
的导函数为 ,则
,则 (
( 为虚数单位)的值为( )
为虚数单位)的值为( )