题目内容
已知A是△ABC的内角，则“cos（π+A）=-
”是“sin（π-A）=
”的
- A.充要条件
- B.充分不必要条件
- C.必要不充分条件
- D.既不充分又不必要条件
B
分析：由cos（π+A）=-，利用A是△ABC的内角，可得A=
，从而sin（π-A）=；当sin（π-A）=时，由A是△ABC的内角，可得A=或
，从而cos（π+A）=-或，故可得结论．
解答：当cos（π+A）=-时，cosA=，∵A是△ABC的内角，∴A=，此时，sin（π-A）=sin=；
当sin（π-A）=时，sinA=，A是△ABC的内角，∴A=或，此时cos（π+A）=-或，
∴“cos（π+A）=-”是“sin（π-A）=”的充分不必要条件
故选B．
点评：本题考查充要条件的判定，考查三角函数知识，属于基础题．
分析：由cos（π+A）=-
，利用A是△ABC的内角，可得A=，从而sin（π-A）=；当sin（π-A）=时，由A是△ABC的内角，可得A=或，从而cos（π+A）=-或，故可得结论．解答：当cos（π+A）=-
时，cosA=，∵A是△ABC的内角，∴A=，此时，sin（π-A）=sin=；当sin（π-A）=
时，sinA=，A是△ABC的内角，∴A=或，此时cos（π+A）=-或，∴“cos（π+A）=-
”是“sin（π-A）=”的充分不必要条件故选B．
点评：本题考查充要条件的判定，考查三角函数知识，属于基础题．
练习册系列答案
相关题目
已知P是△ABC所在平面内一点，
+
+2
=
，现将一粒黄豆随机撒在△ABC内，则黄豆落在△APC内的概率是（ ）
| PB |
| PC |
| PA |
| 0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
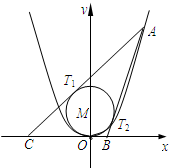已知A是抛物线