题目内容
已知椭圆 (a>b>0)右顶点到右焦点的距离为
(a>b>0)右顶点到右焦点的距离为 ,短轴长为
,短轴长为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过左焦点F的直线与椭圆分别交于A、B两点,若线段AB的长为 ,求直线AB的方程.
,求直线AB的方程.
解:(Ⅰ)由题意, ,解得a=
,解得a= ,c=1.
,c=1.
∴椭圆方程为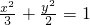 ------------(4分)
------------(4分)
(Ⅱ)当直线AB与x轴垂直时,|AB|= ,不符合题意故舍掉;-----------(6分)
,不符合题意故舍掉;-----------(6分)
当直线AB与x轴不垂直时,设直线AB的方程为:y=k(x+1),
代入消去y得:(2+3k2)x2+6k2x+(3k2-6)=0.
设A(x1,y1),B(x2,y2),则x1+x2= ,x1x2=
,x1x2= -----------(8分)
-----------(8分)
所以|AB|=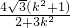 ,------------(11分)
,------------(11分)
∵线段AB的长为 ,
,
∴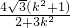 =
=
∴k2=2
∴k= ,------------(13分)
,------------(13分)
所以直线AB的方程为: 或
或 .---------(14分)
.---------(14分)
分析:(Ⅰ)由椭圆 (a>b>0)右顶点到右焦点的距离为
(a>b>0)右顶点到右焦点的距离为 ,短轴长为
,短轴长为 ,建立方程组,即可求得椭圆方程;
,建立方程组,即可求得椭圆方程;
(Ⅱ)当直线AB与x轴垂直时,|AB|= ,不符合题意;当直线AB与x轴不垂直时,设直线AB的方程为:y=k(x+1),代入消去y,利用韦达定理计算|AB|,结合线段AB的长为
,不符合题意;当直线AB与x轴不垂直时,设直线AB的方程为:y=k(x+1),代入消去y,利用韦达定理计算|AB|,结合线段AB的长为 ,即可求得k的值,从而可得直线AB的方程.
,即可求得k的值,从而可得直线AB的方程.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查弦长的计算,联立方程,正确运用韦达定理是关键.
 ,解得a=
,解得a= ,c=1.
,c=1.∴椭圆方程为
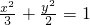 ------------(4分)
------------(4分)(Ⅱ)当直线AB与x轴垂直时,|AB|=
 ,不符合题意故舍掉;-----------(6分)
,不符合题意故舍掉;-----------(6分)当直线AB与x轴不垂直时,设直线AB的方程为:y=k(x+1),
代入消去y得:(2+3k2)x2+6k2x+(3k2-6)=0.
设A(x1,y1),B(x2,y2),则x1+x2=
 ,x1x2=
,x1x2= -----------(8分)
-----------(8分)所以|AB|=
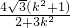 ,------------(11分)
,------------(11分)∵线段AB的长为
 ,
,∴
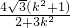 =
=
∴k2=2
∴k=
 ,------------(13分)
,------------(13分)所以直线AB的方程为:
 或
或 .---------(14分)
.---------(14分)分析:(Ⅰ)由椭圆
 (a>b>0)右顶点到右焦点的距离为
(a>b>0)右顶点到右焦点的距离为 ,短轴长为
,短轴长为 ,建立方程组,即可求得椭圆方程;
,建立方程组,即可求得椭圆方程;(Ⅱ)当直线AB与x轴垂直时,|AB|=
 ,不符合题意;当直线AB与x轴不垂直时,设直线AB的方程为:y=k(x+1),代入消去y,利用韦达定理计算|AB|,结合线段AB的长为
,不符合题意;当直线AB与x轴不垂直时,设直线AB的方程为:y=k(x+1),代入消去y,利用韦达定理计算|AB|,结合线段AB的长为 ,即可求得k的值,从而可得直线AB的方程.
,即可求得k的值,从而可得直线AB的方程.点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查弦长的计算,联立方程,正确运用韦达定理是关键.

练习册系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程. (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. 分)
分) (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点. 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.