题目内容
20.已知M=$\frac{{C}_{2015}^{0}}{1}$-$\frac{{C}_{2015}^{1}}{2}$+$\frac{{C}_{2013}^{2}}{3}$-$\frac{{C}_{2015}^{3}}{4}$+…+$\frac{{C}_{2015}^{2014}}{2015}$-$\frac{{C}_{2015}^{2015}}{2016}$,则M的值为$\frac{1}{2016}$.分析 展开二项式(1-x)2015,然后两边取0到1上的积分得答案.
解答 解:∵$(1-x)^{2015}={C}_{2015}^{0}-{C}_{2015}^{1}x+{C}_{2015}^{2}{x}^{2}$$-{C}_{2015}^{3}{x}^{3}+…+$${C}_{2015}^{2014}{x}^{2014}-{C}_{2015}^{2015}{x}^{2015}$,
两边取积分得:
${∫}_{0}^{1}(1-x)^{2015}dx$=${∫}_{0}^{1}({C}_{2015}^{0}-{C}_{2015}^{1}x+{C}_{2015}^{2}{x}^{2}-{C}_{2015}^{3}{x}^{3}+…+{C}_{2015}^{2014}{x}^{2014}-{C}_{2015}^{2015}{x}^{2015})dx$,
即$(\frac{{C}_{2015}^{0}x}{1}-\frac{{C}_{2015}^{1}{x}^{2}}{2}+…+\frac{{C}_{2015}^{2014}{x}^{2015}}{2015}-\frac{{C}_{2015}^{2015}{x}^{2016}}{2016}){|}_{0}^{1}$=$-\frac{1}{2016}(1-x)^{2016}{|}_{0}^{1}$,
∴M=$\frac{{C}_{2015}^{0}}{1}$-$\frac{{C}_{2015}^{1}}{2}$+$\frac{{C}_{2015}^{2}}{3}$-$\frac{{C}_{2015}^{3}}{4}$+…+$\frac{{C}_{2015}^{2014}}{2015}$-$\frac{{C}_{2015}^{2015}}{2016}$=$\frac{1}{2016}$,
故答案为:$\frac{1}{2016}$.
点评 本题考查组合及组合数公式,考查了利用定积分求组合数的值,是中档题.

| A. | ($\frac{\sqrt{5}-1}{2}$,$\frac{\sqrt{2}}{2}$) | B. | ($\frac{\sqrt{5}-1}{2}$,1) | C. | (0,$\frac{\sqrt{5}-1}{2}$) | D. | ($\frac{\sqrt{2}}{2}$,1) |
| A. | 65 | B. | 80 | C. | 85 | D. | 170 |
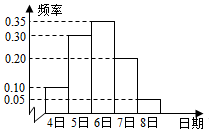 北京铁路局针对今年春运客流量进行数据整理,调查北京西站从2月4日到2月8日的客流量,根据所得数据画出了五天中每日客流量的频率分布图,为了更详细地分析不同时间的客流人群,按日期用分层抽样的方法抽样,若从2月7日这个日期抽取了40人,则一共抽取的人数为200.
北京铁路局针对今年春运客流量进行数据整理,调查北京西站从2月4日到2月8日的客流量,根据所得数据画出了五天中每日客流量的频率分布图,为了更详细地分析不同时间的客流人群,按日期用分层抽样的方法抽样,若从2月7日这个日期抽取了40人,则一共抽取的人数为200.