题目内容
过双曲线 上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则
上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则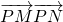 =________.
=________.
a2
分析:先设P坐标,再求出M,N的坐标,最后利用向量数量积的坐标运算解决.
解答:设P(x0,y0),则过P与实轴平行的直线为y=y0,与 双曲线的两条渐近线方程 y=± 分别联立,解得M(
分别联立,解得M( y0,y0),N(-
y0,y0),N(- y0,y0)∴
y0,y0)∴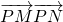 =(
=( ,0)•(-
,0)•(- ,0)=x02-
,0)=x02- =a2(
=a2( )=a2.
)=a2.
故答案为:a2
点评:本体考查双曲线的简单几何性质中的实轴,渐近线.同时考查了向量的数量积这一重要概念.
分析:先设P坐标,再求出M,N的坐标,最后利用向量数量积的坐标运算解决.
解答:设P(x0,y0),则过P与实轴平行的直线为y=y0,与 双曲线的两条渐近线方程 y=±
 分别联立,解得M(
分别联立,解得M( y0,y0),N(-
y0,y0),N(- y0,y0)∴
y0,y0)∴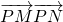 =(
=( ,0)•(-
,0)•(- ,0)=x02-
,0)=x02- =a2(
=a2( )=a2.
)=a2.故答案为:a2
点评:本体考查双曲线的简单几何性质中的实轴,渐近线.同时考查了向量的数量积这一重要概念.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 上任意一点P作x轴的平行线交两条渐近线于Q,R两点,则
上任意一点P作x轴的平行线交两条渐近线于Q,R两点,则 = .
= . 上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则
上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则 的值为( )
的值为( ) 上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则
上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则 = .
= . 上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则
上任意一点P,引与实轴平行的直线,交两渐近线于M、N两点,则 的值为( )
的值为( )