题目内容
过椭圆
（a＞b＞0）的左焦点F1作直线交椭圆于点A，B．F2为右焦点，则△ABF2的周长为
- A.2a
- B.4a
- C.2b
- D.4b
B
分析：先由椭圆方程求得长半轴，而△ABF2的周长为AB+BF2+AF2，由椭圆的定义求解即可．
解答：∵椭圆
根据椭圆的定义
AF1+AF2=2a
∴BF1+BF2=2a
∵AF1+BF1=AB
∴△ABF2的周长为4a；
故选B
点评：本题主要考查椭圆的定义的应用，应用的定义的基本特征，是与焦点有关．
分析：先由椭圆方程求得长半轴，而△ABF2的周长为AB+BF2+AF2，由椭圆的定义求解即可．
解答：∵椭圆
根据椭圆的定义
AF1+AF2=2a
∴BF1+BF2=2a
∵AF1+BF1=AB
∴△ABF2的周长为4a；
故选B
点评：本题主要考查椭圆的定义的应用，应用的定义的基本特征，是与焦点有关．
练习册系列答案
相关题目
=1(a＞b＞0)的左焦点F任作一条与两坐标轴都不垂直的弦AB，若点M在x轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”，那么“左特征点”M一定是（ ）
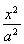
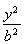
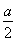
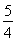
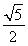
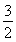
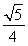
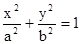（a＞b＞0）的左焦点F1的弦，则⊿ABF2的周长是（ ）
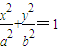（a＞b＞0）的焦点且垂直于x轴的直线被椭圆截得的线段长为
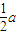，则该椭圆的离心率是（ ）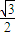
，（a＞b＞0）的两焦点分别为F1、F2，
，离心率
．过直线l：
上任意一点M，引椭圆C的两条切线，切点为A、B．
（a＞b＞0），上一点P（x，y）处的切线方程”（只写类比结论，不必证明）．
）；