题目内容
长方体ABCD—A1B1C1D1中,已知AB=a,BC=b,AA1=c,且a>b,求:(1)下列异面直线之间的距离:AB与CC1;AB与A1C1;AB与B1C.
(2)异面直线D1B与AC所成角的余弦值.
(1)解:BC为异面直线AB与CC1的公垂线段,故AB与CC1的距离为b.
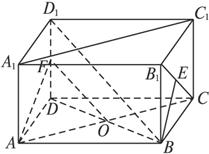
AA1为异面直线AB与A1C1的公垂线段,故AB与A1C1的距离为c.过B作BE⊥B1C,垂足为E,则BE为异面直线AB与B1C的公垂线,BE=![]() =
=![]() ,即AB与B1C的距离为
,即AB与B1C的距离为![]() .
.
(2)解法一:连结BD交AC于点O,取DD1的中点F,连结OF、AF,则OF∥D1B,∴∠AOF就是异面直线D1B与AC所成的角.
∵AO=![]() ,OF=
,OF=![]() BD1=
BD1=![]() ,AF=
,AF=![]() ,
,
∴在△AOF中,cos∠AOF=![]() =
=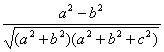 .
.
解法二:如下图,在原长方体的右侧补上一个同样的长方体,连结BG、D1G,则AC∥BG,
∴∠D1BG(或其补角)为D1B与AC所成的角.
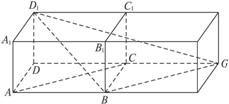
BD1=![]() ,BG=
,BG=![]() ,D1G=
,D1G=![]() ,
,
在△D1BG中,cos∠D1BG=![]() =-
=-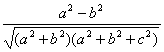 ,
,
故所求的余弦值为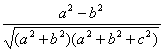 .
.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
长方体ABCD-A1B1C1D1中,AB=3,BC=4,AA1=5 则三棱锥A1-ABC的体积为( )
| A、10 | B、20 | C、30 | D、35 |
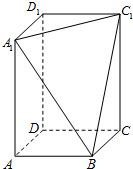 在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.
在长方体ABCD-A1B1C1D1中,AB=BC=2,过A1、C1、B三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD-A1C1D1,且这个几何体的体积为10.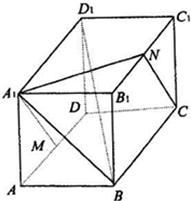 如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC=
如图,长方体ABCD-A1B1C1D1中,AB=A1A=a,BC= 如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点.
如图,已知多面体ABCD-A1B1C1D1,它是由一个长方体ABCD-A'B'C'D'切割而成,这个长方体的高为b,底面是边长为a的正方形,其中顶点A1,B1,C1,D1均为原长方体上底面A'B'C'D'各边的中点. 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E是侧棱BB1的中点.