题目内容
设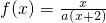 ,方程f(x)=x有唯一解,已知f(xn)=xn+1(n∈N+),且
,方程f(x)=x有唯一解,已知f(xn)=xn+1(n∈N+),且 .
.
(Ⅰ)求证:数列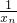 为等差数列,并求数列{xn}的通项公式;
为等差数列,并求数列{xn}的通项公式;
(Ⅱ)若 ,且
,且 (n∈N+),求数列{bn}的前n项和Sn.
(n∈N+),求数列{bn}的前n项和Sn.
(本小题满分12分)
(Ⅰ)f(x)=x变形为 x=0或 ,
,
∴ 的解为x=0
的解为x=0
解得: ,
,
∴ …(2分)
…(2分)
f(xn)=xn+1,即 ,
,
∴ ,
,
∴{ }为公差为
}为公差为 的等差数列,…(4分)
的等差数列,…(4分)
∴ ,
,
∴ …(6分)
…(6分)
(Ⅱ) …(7分)
…(7分)
 …(10分)
…(10分)
∴ .…(12分)
.…(12分)
分析:(Ⅰ)f(x)=x变形为 x=0或 ,解得
,解得 ,故
,故 ,
, ,由此能证明数列
,由此能证明数列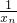 为等差数列,并能求出数列{xn}的通项公式.
为等差数列,并能求出数列{xn}的通项公式.
(Ⅱ)由 ,得
,得 ,由此能求出数列{bn}的前n项和Sn.
,由此能求出数列{bn}的前n项和Sn.
点评:本题考查等差数列的证明,考查数列的通项公式和前n项和的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.
(Ⅰ)f(x)=x变形为 x=0或
 ,
,∴
 的解为x=0
的解为x=0解得:
 ,
,∴
 …(2分)
…(2分)f(xn)=xn+1,即
 ,
,∴
 ,
,∴{
 }为公差为
}为公差为 的等差数列,…(4分)
的等差数列,…(4分)∴
 ,
,∴
 …(6分)
…(6分)(Ⅱ)
 …(7分)
…(7分) …(10分)
…(10分)∴
 .…(12分)
.…(12分)分析:(Ⅰ)f(x)=x变形为 x=0或
 ,解得
,解得 ,故
,故 ,
, ,由此能证明数列
,由此能证明数列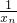 为等差数列,并能求出数列{xn}的通项公式.
为等差数列,并能求出数列{xn}的通项公式.(Ⅱ)由
 ,得
,得 ,由此能求出数列{bn}的前n项和Sn.
,由此能求出数列{bn}的前n项和Sn.点评:本题考查等差数列的证明,考查数列的通项公式和前n项和的求法,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目