题目内容
已知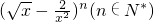 的展开式中第五项系数与第三项的系数的比是10,
的展开式中第五项系数与第三项的系数的比是10,
(1)求n的值;
(2)求展开式中含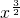 的项;
的项;
(3)求有理项共有多少项.
解:(1)由题意得: ,∴n2-5n-24=0,解得n=8.(4分)
,∴n2-5n-24=0,解得n=8.(4分)
(2)Tr+1= ,令
,令 ,得r=1,
,得r=1,
∴T2= ..(3分)
..(3分)
(3)令 则r=0或r=2或r=4或r=6或r=8
则r=0或r=2或r=4或r=6或r=8
所以有理项共5项.(10分).
分析:(1)已知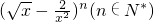 的展开式中第五项系数与第三项的系数的比是10,由此关系建立起方程,求出n;
的展开式中第五项系数与第三项的系数的比是10,由此关系建立起方程,求出n;
(2)由(1),n=8,利用展开式中项的公式Tr+1=Cnr( )n-r(
)n-r( )r=
)r= ,令x的指数为
,令x的指数为 解出r,即得项;
解出r,即得项;
(3)对展开式中的指数进行研究,得出可使指数为整数的r的值.
点评:本题考查二项式的性质,解题的关键是熟练掌握二项展开式,且能由题意将题设条件中的关系转化为关于参数的方程,本题考查转化化归的能力及运算能力.
 ,∴n2-5n-24=0,解得n=8.(4分)
,∴n2-5n-24=0,解得n=8.(4分)(2)Tr+1=
 ,令
,令 ,得r=1,
,得r=1,∴T2=
 ..(3分)
..(3分)(3)令
 则r=0或r=2或r=4或r=6或r=8
则r=0或r=2或r=4或r=6或r=8所以有理项共5项.(10分).
分析:(1)已知
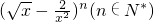 的展开式中第五项系数与第三项的系数的比是10,由此关系建立起方程,求出n;
的展开式中第五项系数与第三项的系数的比是10,由此关系建立起方程,求出n;(2)由(1),n=8,利用展开式中项的公式Tr+1=Cnr(
 )n-r(
)n-r( )r=
)r= ,令x的指数为
,令x的指数为 解出r,即得项;
解出r,即得项;(3)对展开式中的指数进行研究,得出可使指数为整数的r的值.
点评:本题考查二项式的性质,解题的关键是熟练掌握二项展开式,且能由题意将题设条件中的关系转化为关于参数的方程,本题考查转化化归的能力及运算能力.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 的展开式中第五项的系数与第三项的系数的比是10:1.
的展开式中第五项的系数与第三项的系数的比是10:1. 的展开式中第五项的系数与第三项的系数的比是10:1
的展开式中第五项的系数与第三项的系数的比是10:1 的项;
的项; 的展开式中第五项的系数与第三项的系数的比是10:1.
的展开式中第五项的系数与第三项的系数的比是10:1. 的展开式中第五项的系数与第三项的系数之比是10︰1,求展开式中x的系数.
的展开式中第五项的系数与第三项的系数之比是10︰1,求展开式中x的系数. 的展开式中第五项的系数与第三项的系数比是10:1.
的展开式中第五项的系数与第三项的系数比是10:1. 的项的系数; (2)求:展开式中所有项系数的绝对值之和.
的项的系数; (2)求:展开式中所有项系数的绝对值之和.