Question

在△ABC中,∠A=60°，且∠A的平分线AD将BC分成两段之比为BD∶DC=2∶1，又AD=。

（1）求三边长；

（2）求角C.

Answer 1

（1）解法一：∵∠A的平分线AD将BC分成两段比为BD∶DC=2∶1，则AB∶AC=2∶1，设AB=2x，AC=x,

由S_△ABD+S_△ADC=S_△ABC可知·c·AD·sin+·b·AD·sin=bc·sinA,

∴AD=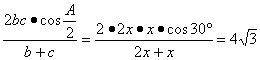,解得x=6.

∴AC=6,AB=12.

由余弦定理得BC²=6²+12²-2·6·12·cos60°=108.

∴BC=.

解法二：由题意知.如图，设AB=2y,BD=2x,则AC=y,CD=x.

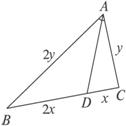
由余弦定理得

即

∴AB=12,AC=6,BC=.

（2）解：由余弦定理得cosC==0,故C=90°.