题目内容
已知椭圆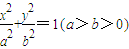
的离心率为
，若将这个椭圆绕着它的右焦点按逆时针方向旋转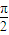
后，所得新椭圆的一条准线方程是
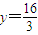，则原来的椭圆方程是 ；新椭圆方程是 ．
【答案】分析：先根据离心率和新椭圆的准线方程求出a，b，c的值，代入可直接求出原来方程；对于新椭圆方程，要先找到中心然后根据a，b，c没发生改变可得到答案．
解答：解：由题意可知，e=
，y=
-c=
∵a2=b2+c2
∴c=3，a=5，b=4
原椭圆方程为
新椭圆方程为：
故答案为：
，
点评：本题主要考查椭圆方程的标准方程．对于椭圆方程要知道离心率e=
，准线为y=
（焦点在x轴）．
解答：解：由题意可知，e=
，y=-c=∵a2=b2+c2∴c=3，a=5，b=4
原椭圆方程为
新椭圆方程为：
故答案为：
，点评：本题主要考查椭圆方程的标准方程．对于椭圆方程要知道离心率e=
，准线为y=（焦点在x轴）． 
练习册系列答案
相关题目
已知椭圆的离心率为e，两焦点分别为F1、F2，抛物线C以F1为顶点、F2为焦点，点P为抛物线和椭圆的一个交点，若e|PF2|=|PF1|，则e的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
，焦点是（-3，0），（3，0），则椭圆方程为（ ）
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在由圆O：x2+y2=1和椭圆C：
如图，A，B是椭圆C：