题目内容
若将函数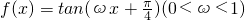 的图象向右平移
的图象向右平移 个单位长度后与函数
个单位长度后与函数 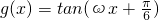 的图象重合,则函数y=f(x)的一个对称中心为
的图象重合,则函数y=f(x)的一个对称中心为
- A.(
 ,0)
,0) - B.(
 ,0)
,0) - C.(
 ,0)
,0) - D.(π,0)
B
分析:根据图象的平移求出平移后的函数解析式,与函数y=tan(ωx+ )的图象重合,比较系数,求出ω=6k+
)的图象重合,比较系数,求出ω=6k+ (k∈Z),然后代入已知函数解析式中可求
(k∈Z),然后代入已知函数解析式中可求
解答:y=tan(ωx+ ),向右平移
),向右平移 个单位可得:y=tan[ω(x-
个单位可得:y=tan[ω(x- )+
)+ ]=tan(ωx+
]=tan(ωx+ )
)
∴ -
- ω+kπ=
ω+kπ=
∴ω=6k+ (k∈Z),
(k∈Z),
又∵1>ω>0
∴当k=0时,ω= ,f(x)=tan(
,f(x)=tan(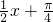 )
)
令 ,k∈Z可得x=
,k∈Z可得x= ,k∈Z
,k∈Z
当k=1时,x=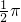 ,一个对称中心(
,一个对称中心( )
)
故选B
点评:本题主要考查了三角函数的图象的平移,正切函数的对称性质的考查,属于三角函数性质的简单应用.
分析:根据图象的平移求出平移后的函数解析式,与函数y=tan(ωx+
 )的图象重合,比较系数,求出ω=6k+
)的图象重合,比较系数,求出ω=6k+ (k∈Z),然后代入已知函数解析式中可求
(k∈Z),然后代入已知函数解析式中可求解答:y=tan(ωx+
 ),向右平移
),向右平移 个单位可得:y=tan[ω(x-
个单位可得:y=tan[ω(x- )+
)+ ]=tan(ωx+
]=tan(ωx+ )
)∴
 -
- ω+kπ=
ω+kπ=
∴ω=6k+
 (k∈Z),
(k∈Z),又∵1>ω>0
∴当k=0时,ω=
 ,f(x)=tan(
,f(x)=tan(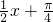 )
)令
 ,k∈Z可得x=
,k∈Z可得x= ,k∈Z
,k∈Z当k=1时,x=
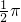 ,一个对称中心(
,一个对称中心( )
)故选B
点评:本题主要考查了三角函数的图象的平移,正切函数的对称性质的考查,属于三角函数性质的简单应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
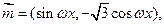
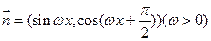 ,若函数
,若函数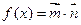 的最小正周期为
的最小正周期为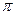
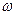 的值
的值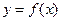 的图象向右平移
的图象向右平移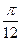 个单位,再将所得到的图象上各点的横坐标伸长到原来的
个单位,再将所得到的图象上各点的横坐标伸长到原来的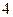 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数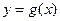 的图象,求
的图象,求 的图象向右平移
的图象向右平移 个单位长度后,与函数
个单位长度后,与函数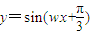 的图象重合,则w的最小值为( )
的图象重合,则w的最小值为( )
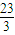
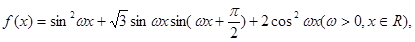 在
在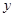 轴右侧的第一个最高点的横坐标为
轴右侧的第一个最高点的横坐标为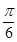 .
.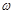 的值;
的值;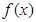 的图象向右平移
的图象向右平移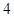 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数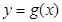 的图象,求函数
的图象,求函数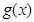 的最大值及单调递减区间.
的最大值及单调递减区间.
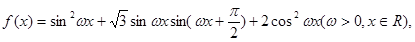 在
在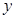 轴右侧的第一个最高点的横坐标为
轴右侧的第一个最高点的横坐标为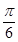 .
.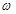 的值;
的值;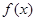 的图象向右平移
的图象向右平移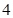 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数 的图象,求函数
的图象,求函数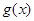 的最大值及单调递减区间.
的最大值及单调递减区间. ,在
,在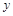 轴右侧的第一个最高点的横标为
轴右侧的第一个最高点的横标为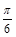 .
.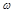 ;
;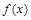 的图象向右平移
的图象向右平移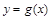 的图象,求函数
的图象,求函数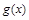 的最大值及单位递减区间.
的最大值及单位递减区间.