题目内容
已知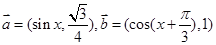
，函数
.
（1）求
的最值和单调递减区间；
（2）已知在△ABC中，角A、B、C的对边分别为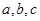
，
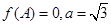，求△ABC的面积的最大值.
【答案】
（1）
的最大值为
，最小值为
，单调递减区间为
；
（2）
.
【解析】
试题分析：（1）先由向量数量积得
表达式，经过三角恒等变换将其化为一个角的三角函数，最终可得的最大最小值和单调递减区间；（2）在（1）的基础上先求出
的值，利用余弦定理可得
，再利用重要不等式
得
的范围，最后利用
求得
面积的最大值.
试题解析：
（1）
2分
.
4分
令
，
解得
单调递减区间为. 6分
（2）
． 8分
由余弦定理得，
．
又
.
10分
.
12分
考点：1、向量数量积运算；2、三角恒等变换及三角函数性质；3、解三角形；4、重要不等式．
练习册系列答案
相关题目
已知以下函数：（1）f（x）=3lnx；（2）f（x）=3ecosx；（3）f（x）=3ex；（4）f（x）=3cosx．
其中对于f（x）定义域内的任意一个自变量x1，都存在唯一一个自变量x2使
=3成立的函数是（ ）
其中对于f（x）定义域内的任意一个自变量x1，都存在唯一一个自变量x2使
| f(x1)f(x2) |
| A、（1）（2）（4） |
| B、（2）（3） |
| C、（3） |
| D、（4） |
已知分段函数f(x)=
，则
f(x-2)dx等于（ ）
|
| ∫ | 3 1 |
A、
| ||||
| B、2-e | ||||
C、3+
| ||||
D、2-
|
已知符号函数sgn x=
则方程x+1=（2x-1）sgnx的所有解之和是（ ）
|
| A、0 | ||||
| B、2 | ||||
C、-
| ||||
D、
|