题目内容
若数列{an}为等比数列,则”a3•a5=16”是”a4=4”的
- A.充分不必要条件
- B.必要不充分条件
- C.充分必要条件
- D.既不充分也不必要条件
B
分析:由等比数列的性质判断出a3•a5=a42成立推不出”a4=4”成立,反之”a4=4”成立能推出”a3•a5=16”成立;利用充要条件的有关定义得到结论.
解答:若”a3•a5=16”成立,由等比数列的性质得到”a3•a5=a42,所以a42=16,所以a4=±4;
反之,当”a4=4”成立,由等比数列的性质得到”a3•a5=a42,所以a3•a5=16”;
所以”a3•a5=16”是”a4=4”的必要不充分条件
故选B.
点评:判断一个命题是另一个命题的什么条件,应该确定好条件,然后两边互推一下,利用充要条件的有关定义加以判断.
分析:由等比数列的性质判断出a3•a5=a42成立推不出”a4=4”成立,反之”a4=4”成立能推出”a3•a5=16”成立;利用充要条件的有关定义得到结论.
解答:若”a3•a5=16”成立,由等比数列的性质得到”a3•a5=a42,所以a42=16,所以a4=±4;
反之,当”a4=4”成立,由等比数列的性质得到”a3•a5=a42,所以a3•a5=16”;
所以”a3•a5=16”是”a4=4”的必要不充分条件
故选B.
点评:判断一个命题是另一个命题的什么条件,应该确定好条件,然后两边互推一下,利用充要条件的有关定义加以判断.

练习册系列答案
相关题目
 0,b
0,b 时,
时,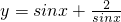 的最小值是
的最小值是 .
. (k为常数),则称数列{an}为等比和数列,k称为公比和.已知数列{an}是以3为公比和的等比和数列,其中a1=1,a2=2,则a2009= .
(k为常数),则称数列{an}为等比和数列,k称为公比和.已知数列{an}是以3为公比和的等比和数列,其中a1=1,a2=2,则a2009= .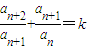 (k为常数),则称数列{an}为等比和数列,k称为公比和.已知数列{an}是以3为公比和的等比和数列,其中a1=1,a2=2,则a2009= .
(k为常数),则称数列{an}为等比和数列,k称为公比和.已知数列{an}是以3为公比和的等比和数列,其中a1=1,a2=2,则a2009= .