题目内容
17.已知数列{an}(n∈N*),若{an+an+1}为等比数列,则称{an}具有性质P.(1)若数列{an}具有性质P,且a1=a2=1,a3=3,求a4、a5的值;
(2)若bn=2n+(-1)n,求证:数列{bn}具有性质P;
(3)设c1+c2+…+cn=n2+n,数列{dn}具有性质P,其中d1=1,d3-d2=c1,d2+d3=c2,若dn>102,求正整数n的取值范围.
分析 (1){an+an+1}为等比数列,由a1=a2=1,a3=3,可得{an+an+1}的公比为2,可得an+an+1=2n,进而得出a4、a5的值;
(2)证明{bn+bn+1}是以公比为2的等比数列,即可得出结论;
(3)求出dn+dn+1=2n,利用dn>102,求正整数n的取值范围.
解答 解:(1){an+an+1}为等比数列,
∵a1=a2=1,a3=3,
∴a1+a2=1+1=2,a2+a3=1+3=4,
∴{an+an+1}的公比为2,
∴an+an+1=2n,
∴a3+a4=23=8,即a4=5,
∴a4+a5=24=16,即a5=11;
(2)∵bn=2n+(-1)n,
∴bn+bn+1=2n+(-1)n+2n+1+(-1)n+1=3•2n,
∴{bn+bn+1}是以公比为2的等比数列,
∴数列{bn}具有性质P.
(3)∵c1+c2+…+cn=n2+n,
∴c1+c2+…+cn-1=(n-1)2+n-1,
∴cn=2n,
∵d1=1,d3-d2=c1=2,d2+d3=c2=4,
∴d2=1,d3=3,
∵数列{dn}具有性质P,
由(1)可得,dn+dn+1=2n,∴d4=5,d5=11,d6=21,d7=43,d8=85,d9=171,
∵dn>102,∴正整数n的取值范围是[9,+∞).
点评 本题考查新定义,考查等比数列的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
2.函数f(x)=$\frac{2sinx•cosx}{1+sinx+cosx}$,x∈(0,$\frac{π}{2}$]的最大值M,最小值为N,则M-N=( )
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\sqrt{2}$-1 | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$+1 |
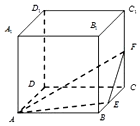 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段AP长度的取值范围是[$\frac{3\sqrt{2}}{4}$,$\frac{\sqrt{5}}{2}$].
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段AP长度的取值范围是[$\frac{3\sqrt{2}}{4}$,$\frac{\sqrt{5}}{2}$].