题目内容
由抛物线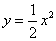 与直线
与直线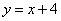 所围成的图形的面积是
所围成的图形的面积是
A.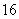 | B.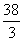 | C.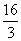 | D.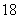 |
D
解析试题分析:抛物线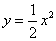 与直线
与直线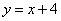 的交点
的交点 ,结合图形可知围成的面积为
,结合图形可知围成的面积为
考点:定积分的几何意义
点评:若函数 满足
满足 ,则
,则 的值等于直线
的值等于直线 与
与 曲线围成的曲边形的面积
曲线围成的曲边形的面积

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知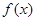 是定义在
是定义在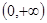 上的非负可导函数,且满足
上的非负可导函数,且满足 ,对任意正数
,对任意正数 ,若
,若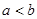 ,则
,则 的大小关系为
的大小关系为
A. | B.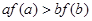 |
C.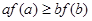 | D. |
已知 在R上可导,且
在R上可导,且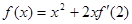 ,则
,则 的大小关系是( )
的大小关系是( )
A.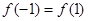 | B. |
C. | D.不确定 |
已知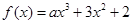 ,若
,若 ,则a的值等于 ( )
,则a的值等于 ( )
A.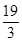 | B. | C.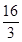 | D.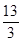 |
已知 ,则
,则 ( )
( )
A. | B. | C. | D. |
函数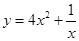 的单调递增区间为( )
的单调递增区间为( )
A.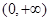 | B. | C. | D.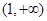 |
设 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,当
,当 时,有
时,有 恒成立,则不等式
恒成立,则不等式 的解集是 ( )
的解集是 ( )
A. | B. |
C. | D. |
已知 ,其中
,其中 ,如果存在实数
,如果存在实数 ,使
,使 ,则
,则 的值( )
的值( )
| A.必为正数 | B.必为负数 | C.必为非负数 | D.必为非正数 |
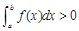 ,则f(x)>0; ⑵
,则f(x)>0; ⑵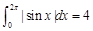 ;⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则
;⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则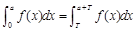 ;其中正确命题的个数为( )
;其中正确命题的个数为( )