题目内容
已知圆C: x2+y2-2x+4y-4=0,是否存在斜率为1的直线L,使以L被圆C截得弦AB为直径的圆经过原点?若存在,写出直线的方程;若不存在,说明理由![]()
解:设直线L的斜率为1,且L的方程为y=x+b,则
 消元得方程2x2+(2b+2)x+b2+4b-4=0,设此方程两根为x1,x2,则x1+x2=-(b+1),y1+y2= x1+x2+2b=b-1,则AB中点为
消元得方程2x2+(2b+2)x+b2+4b-4=0,设此方程两根为x1,x2,则x1+x2=-(b+1),y1+y2= x1+x2+2b=b-1,则AB中点为![]() ,又弦长为
,又弦长为![]() =
=![]() ,由题意可列式
,由题意可列式![]() =
= 解得b=1或b=-9,经检验b=-9不合题意.所以所求直线方程为y=x+1
解得b=1或b=-9,经检验b=-9不合题意.所以所求直线方程为y=x+1![]()


练习册系列答案
相关题目
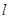 :x-y+2=0的对称点都在圆C上,则a=
.
:x-y+2=0的对称点都在圆C上,则a=
.