Question

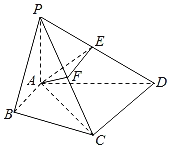
【题目】如图，在菱形中，，点为中点，平面

（1）求证：平面.

（2）若，，求直线与平面所成角的正弦值.

Answer 1

【答案】(1)见解析(2)

【解析】

（1）要证CD⊥平面PAN，可由PA⊥平面ABCD得出CD⊥PA；△ACD为正三角形，点N为CD中点，得出CD⊥AN，且PA∩AN=A而证出．
（2）过A作AH⊥PN于H，则AH⊥平面PCD，连接CH，则∠ACH为直线AC与平面PCD所成角．在RT△ACH中求解即可．

（1）证明：因为四边形ABCD为菱形，∠BAD＝120°，所以△ACD为正三角形，所以AC＝AD，又因为点N为CD中点，所以CD⊥AN．

∵PA⊥平面ABCD，CD平面ABCD，∴CD⊥PA．PA∩AN＝A，∴CD⊥平面PAN．

（2）由（1）知，CD⊥平面PAN，CD平面PCD，∴平面PAN⊥平面PCD，且平面PAN∩平面PCD＝PN，

过A作AH⊥PN于H，则AH⊥平面PCD，连接CH，则∠ACH为直线AC与平面PCD所成角．

在RT△PAN中，PA，AN，由勾股定理得出PN，根据面积相等法得AH．

在RT△ACH中，sin∠ACH．即直线AC与平面PCD所成角的正弦值是．