题目内容
求下列各函数的导数:
(1)y=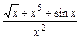 ;
;
(2)y=(x+1)(x+2)(x+3);
(3)y=-sin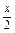 (1-2cos2
(1-2cos2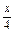 );
);
(4)y=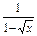 +
+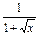 .
.
(1)y=
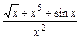 ;
;(2)y=(x+1)(x+2)(x+3);
(3)y=-sin
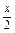 (1-2cos2
(1-2cos2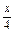 );
);(4)y=
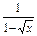 +
+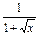 .
.(1)-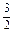 x
x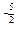 +3x2-2x-3sinx+x-2cosx. (2)3x2+12x+11
+3x2-2x-3sinx+x-2cosx. (2)3x2+12x+11
(3)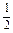 cosx (4)
cosx (4)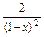
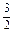 x
x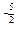 +3x2-2x-3sinx+x-2cosx. (2)3x2+12x+11
+3x2-2x-3sinx+x-2cosx. (2)3x2+12x+11(3)
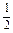 cosx (4)
cosx (4)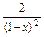
(1)∵y=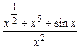 =x
=x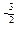 +x3+
+x3+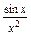 ,
,
∴y′=(x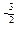 )′+(x3)′+(x-2sinx)′
)′+(x3)′+(x-2sinx)′
=-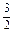 x
x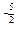 +3x2-2x-3sinx+x-2cosx.
+3x2-2x-3sinx+x-2cosx.
(2)方法一 y=(x2+3x+2)(x+3)
=x3+6x2+11x+6,
∴y′=3x2+12x+11.
方法二
y′=[(x+1)(x+2)]′(x+3)+(x+1)(x+2)(x+3)′
=[(x+1)′(x+2)+(x+1)(x+2)′](x+3)+(x+1)(x+2)
=(x+2+x+1)(x+3)+(x+1)(x+2)
=(2x+3)(x+3)+(x+1)(x+2)
=3x2+12x+11.
(3)∵y=-sin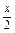 (-cos
(-cos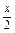 )=
)=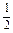 sinx,
sinx,
∴y′=(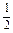 sinx) ′=
sinx) ′= 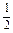 (sinx)′=
(sinx)′=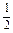 cosx.
cosx.
(4)y=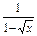 +
+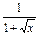 =
=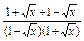 =
=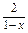 ,
,
∴y′=(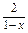 )′=
)′=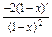 =
=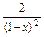 .
.
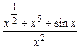 =x
=x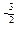 +x3+
+x3+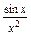 ,
,∴y′=(x
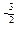 )′+(x3)′+(x-2sinx)′
)′+(x3)′+(x-2sinx)′=-
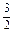 x
x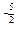 +3x2-2x-3sinx+x-2cosx.
+3x2-2x-3sinx+x-2cosx.(2)方法一 y=(x2+3x+2)(x+3)
=x3+6x2+11x+6,
∴y′=3x2+12x+11.
方法二
y′=[(x+1)(x+2)]′(x+3)+(x+1)(x+2)(x+3)′
=[(x+1)′(x+2)+(x+1)(x+2)′](x+3)+(x+1)(x+2)
=(x+2+x+1)(x+3)+(x+1)(x+2)
=(2x+3)(x+3)+(x+1)(x+2)
=3x2+12x+11.
(3)∵y=-sin
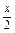 (-cos
(-cos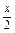 )=
)=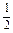 sinx,
sinx,∴y′=(
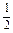 sinx) ′=
sinx) ′= 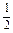 (sinx)′=
(sinx)′=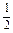 cosx.
cosx.(4)y=
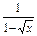 +
+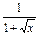 =
=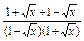 =
=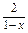 ,
,∴y′=(
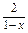 )′=
)′=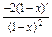 =
=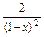 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
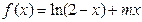 在区间
在区间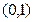 上是增函数.(1)求实数m的取值范围;(2)若数列
上是增函数.(1)求实数m的取值范围;(2)若数列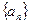 满足
满足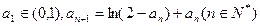 ,证明:
,证明: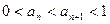 .
.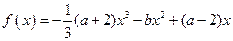 。
。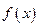 在
在 处取得极值,且
处取得极值,且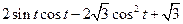 试求实数
试求实数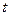 的取值范围;
的取值范围;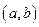 ,试求出点P的轨迹所形成的图形的面积S。
,试求出点P的轨迹所形成的图形的面积S。
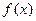 的单调区间; (II)当
的单调区间; (II)当 在区间[—1,2]上是单调函数,求a的取值范围。
在区间[—1,2]上是单调函数,求a的取值范围。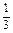 是f(x)的极值点,求f(x)在[1,a]上的最大值;
是f(x)的极值点,求f(x)在[1,a]上的最大值;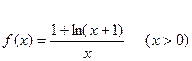 ,
,
 在区间
在区间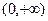 是增函数还是减函数?并证明你的结论;
是增函数还是减函数?并证明你的结论;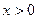 时,
时,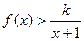 恒成立,求整数
恒成立,求整数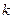 的最小值。
的最小值。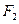 为圆心,过另一焦点
为圆心,过另一焦点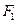 的圆被右准线截的两段弧长之比2:1,
的圆被右准线截的两段弧长之比2:1,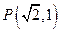 为此平面上一定点,且
为此平面上一定点,且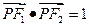 .(1)求椭圆的方程(2)若直线
.(1)求椭圆的方程(2)若直线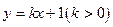 与椭圆交于如图两点A、B,令
与椭圆交于如图两点A、B,令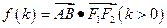 。求函数
。求函数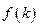 的值域
的值域