题目内容
对于函数y=|x-1|+|x-2|+…+|x-2012|的图象,说法正确的为( )A.图象无对称轴,且在R上不单调
B.图象无对称轴,且在R上单调递增
C.图象有对称轴,且在对称轴右侧不单调
D.图象有对称轴,且在对称轴右侧单调递增
【答案】分析:函数y=|x-1|+|x-2|+…+|x-2012|表示数轴上的x对应点到1,2,3,4…2012的距离之和,f(x)的图象关于直线 x=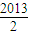 对称如图所示:结合图形得出结论.
对称如图所示:结合图形得出结论.
解答:解:由绝对值的意义可得函数y=|x-1|+|x-2|+…+|x-2012|表示数轴上的x对应点到1,2,3,4…2012的距离之和,
当x∈[1,2012]时,|x-1|+|x-2012|取得最小值等于2011,
当x∈[2,2011]时,|x-2|+|x-2011|取得最小值等于2009,
当x∈[3,2010]时,|x-3|+|x-2010|取得最小值等于2007,
…
当x∈[1006,1007]时,|x-1006|+|x-1007|取得最小值等于1.
故当x∈[1006,1007]时,函数y=|x-1|+|x-2|+…+|x-2012|=(|x-1|+|x-2012|)+(|x-2|+|x-2011|)+(|x-3|+|x-2010|)+…(|x-1006|+|x-1007|)
取得最小值为2011+2009+2007+…+1=10062.
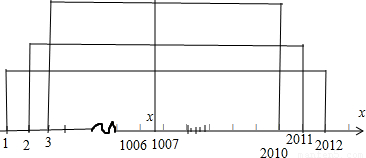
故函数 f(x)的图象关于直线 x=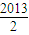 对称.
对称.
当x<1时,函数y=(1-x)+(2-x)+(3-x)+…+(2012-x)=-2012x+2013×1006,
当x>2012时,函数y=(x-1)+(x-2)+(x-3)+…+(x-2012)=2012x-2013×1006,
如图所示:
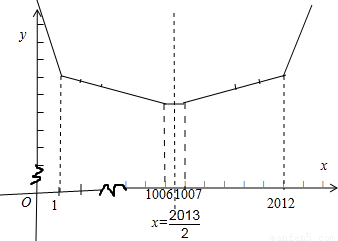
故图象有对称轴,且在对称轴右侧单调递增,
故选D.
点评:本题主要考查绝对值的意义,带有绝对值的函数,体现了数形结合、分类讨论的数学思想,属于中档题.
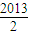 对称如图所示:结合图形得出结论.
对称如图所示:结合图形得出结论.解答:解:由绝对值的意义可得函数y=|x-1|+|x-2|+…+|x-2012|表示数轴上的x对应点到1,2,3,4…2012的距离之和,
当x∈[1,2012]时,|x-1|+|x-2012|取得最小值等于2011,
当x∈[2,2011]时,|x-2|+|x-2011|取得最小值等于2009,
当x∈[3,2010]时,|x-3|+|x-2010|取得最小值等于2007,
…
当x∈[1006,1007]时,|x-1006|+|x-1007|取得最小值等于1.
故当x∈[1006,1007]时,函数y=|x-1|+|x-2|+…+|x-2012|=(|x-1|+|x-2012|)+(|x-2|+|x-2011|)+(|x-3|+|x-2010|)+…(|x-1006|+|x-1007|)
取得最小值为2011+2009+2007+…+1=10062.

故函数 f(x)的图象关于直线 x=
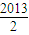 对称.
对称.当x<1时,函数y=(1-x)+(2-x)+(3-x)+…+(2012-x)=-2012x+2013×1006,
当x>2012时,函数y=(x-1)+(x-2)+(x-3)+…+(x-2012)=2012x-2013×1006,
如图所示:

故图象有对称轴,且在对称轴右侧单调递增,
故选D.
点评:本题主要考查绝对值的意义,带有绝对值的函数,体现了数形结合、分类讨论的数学思想,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目