题目内容
如图所示，等腰直角三角形ABC中，∠A=90°，BC=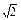
，DA⊥AC，DA⊥AB，若DA=1，且E为DA的中点.求异面直线BE与CD所成角的余弦值.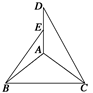
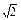，DA⊥AC，DA⊥AB，若DA=1，且E为DA的中点.求异面直线BE与CD所成角的余弦值.异面直线BE与CD所成角的余弦值为
取AC的中点F，连接EF，BF，在△ACD中，E、F分别是AD、AC的中点，
∴EF∥CD，
∴∠BEF即为异面直线BE与CD所成的角或其补角.
在Rt△EAB中，AB=AC=1，
AE=
AD=，∴BE=
，
在Rt△EAF中，
AF=AC=，AE=，∴EF=
，
在Rt△BAF中，AB=1，AF=，∴BF=，
在等腰三角形EBF中，
cos∠FEB=
=，
∴异面直线BE与CD所成角的余弦值为.
∴EF∥CD，
∴∠BEF即为异面直线BE与CD所成的角或其补角.
在Rt△EAB中，AB=AC=1，
AE=
AD=，∴BE=， 在Rt△EAF中，
AF=
AC=，AE=，∴EF=，在Rt△BAF中，AB=1，AF=
，∴BF=，在等腰三角形EBF中，
cos∠FEB=
=，∴异面直线BE与CD所成角的余弦值为
.
练习册系列答案
阅读快车系列答案
相关题目
（1）直线EF∥平面ACD;
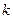个四面体，则
