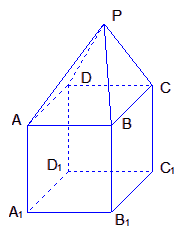
题目内容
在如图组合体中,
![]() 是一个长方体,
是一个长方体,![]() 是一个
是一个
四棱锥;![]() ,点
,点![]() 平面
平面![]() ,且
,且
![]()
(1)证明:![]()
![]() 平面
平面![]()
(2)求![]() 与平面
与平面![]() 所成的角的正切值
所成的角的正切值
证明:⑴因为![]() ,
,![]() ,所以
,所以![]() ,因为
,因为![]() 为长方体,因为
为长方体,因为![]() ,又
,又![]() ,所以
,所以![]() ,故
,故![]() ;
;
⑵取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,因为
,因为![]() ,故面
,故面![]() ,因为
,因为![]() ,面
,面![]() ,所以
,所以![]() ,所以
,所以![]() 即为所求的角,在
即为所求的角,在![]() 中,
中,![]() ,在
,在![]() 中,
中,![]() ,所以
,所以![]() 与平面
与平面![]() 所成的角的正切值是
所成的角的正切值是![]() .
.
解析:
⑴证明线面垂直,常常转化为证明线线垂直;⑵求线面角的关键是找到斜线在平面内的射影,斜线和射影的夹角就是线面角.

练习册系列答案
相关题目
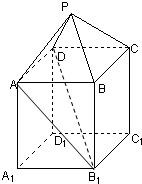 如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且
如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且 (2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=
(2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=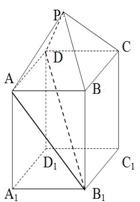 如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=4,BC=3,
如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=4,BC=3,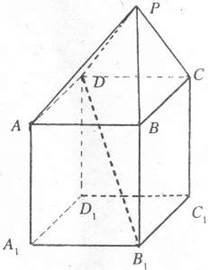 在如图组合体中,
在如图组合体中, 是一个长方体,
是一个长方体,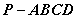 是一个四棱锥。
是一个四棱锥。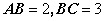 ,
,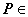 平面
平面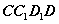 ,且
,且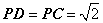 。
。 
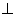 平面
平面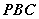 ;
;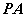 与平面
与平面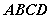 所成的角的正切值;
所成的角的正切值;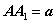 ,当
,当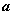 为何值时,
为何值时,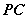
 平面
平面 。
。