题目内容
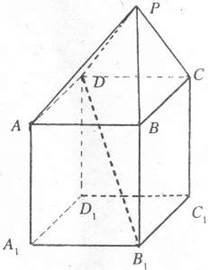 在如图组合体中,
在如图组合体中, 是一个长方体,
是一个长方体,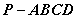 是一个四棱锥。
是一个四棱锥。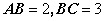 ,
,
点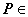 平面
平面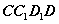 ,且
,且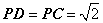 。
。
(1)证明:
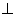 平面
平面 ;
;
(2)求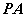 与平面
与平面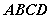 所成的角的正切值;
所成的角的正切值;
(3)若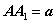 ,当
,当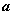 为何值时,
为何值时,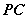
 平面
平面 。
。
【答案】
(1)证明: 为等腰直角三角形且
为等腰直角三角形且 ……1分
……1分 是一个长方体,
是一个长方体, 平面
平面 ,而
,而 平面
平面 ,
, 面
面 ,因而
,因而 。…………3分
。…………3分
 垂直于平面
垂直于平面 内的两条相交直线
内的两条相交直线 和
和 ,由线面垂直的判定定理,可得
,由线面垂直的判定定理,可得 平面
平面 。……………………4分
。……………………4分
(2)解:设 为
为 的中点,连
的中点,连
 是等腰直角三角形,
是等腰直角三角形, 又平面
又平面 平面
平面
 平面
平面 。
。 就是
就是 与平面
与平面 所成的角。……6分
所成的角。……6分
 ………………………7分
………………………7分
 与平面
与平面 所成的角的正切值为
所成的角的正切值为 ………8分
………8分
(3)解:当 时,
时, 平面
平面 ………9分由
………9分由 平面
平面 ,
, 平面
平面 ,平面
,平面 平面
平面
 ,又
,又 平面
平面 ,
, ,因而
,因而 …10分又
…10分又 即
即 是正方形,
是正方形, …………………12分
…………………12分

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
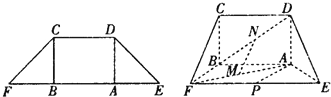 如图,在等腰梯形CDEF中,CB、DA是梯形的高,AE=BF=2,AB=2
如图,在等腰梯形CDEF中,CB、DA是梯形的高,AE=BF=2,AB=2

 (2008•佛山一模)如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且
(2008•佛山一模)如图,在组合体中,ABCD-A1B1C1D1是一个长方体,P-ABCD是一个四棱锥.AB=2,BC=3,点P∈平面CC1D1D且 (2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=
(2012•河北区一模)如图,在三棱柱BCD-B1C1D1与四棱锥A-BB1D1D的组合体中,已知BB1⊥平面BCD,四边形ABCD是平行四边形,∠ABC=120°,AB=