题目内容
椭圆mx2+y2=1的离心率是 ,则它的长半轴的长是
,则它的长半轴的长是
- A.1
- B.1或2
- C.2
- D.
 或1
或1
B
分析:先将椭圆mx2+y2=1的方程可化为: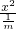 +y2=1,再分类讨论:①当椭圆的焦点在x轴时,②当椭圆的焦点在y轴时,分别求出此时椭圆的长轴长即可.
+y2=1,再分类讨论:①当椭圆的焦点在x轴时,②当椭圆的焦点在y轴时,分别求出此时椭圆的长轴长即可.
解答:椭圆mx2+y2=1的方程可化为: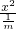 +y2=1,
+y2=1,
①当椭圆的焦点在x轴时,a2= ,b2=1,
,b2=1,
∴c2=a2-b2= -1,
-1,
∴e= =
= =
= =
= ,
,
∴m= ,此时椭圆的长轴长a=
,此时椭圆的长轴长a= =2;
=2;
②当椭圆的焦点在y轴时,
此时椭圆的长轴长a=1;
综上知,长半轴长为1或2
故选B.
点评:本题考查椭圆的性质和标准方程,考查了计算能力的分类讨论思想.属于基础题.
分析:先将椭圆mx2+y2=1的方程可化为:
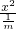 +y2=1,再分类讨论:①当椭圆的焦点在x轴时,②当椭圆的焦点在y轴时,分别求出此时椭圆的长轴长即可.
+y2=1,再分类讨论:①当椭圆的焦点在x轴时,②当椭圆的焦点在y轴时,分别求出此时椭圆的长轴长即可.解答:椭圆mx2+y2=1的方程可化为:
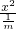 +y2=1,
+y2=1,①当椭圆的焦点在x轴时,a2=
 ,b2=1,
,b2=1,∴c2=a2-b2=
 -1,
-1,∴e=
 =
= =
= =
= ,
,∴m=
 ,此时椭圆的长轴长a=
,此时椭圆的长轴长a= =2;
=2;②当椭圆的焦点在y轴时,
此时椭圆的长轴长a=1;
综上知,长半轴长为1或2
故选B.
点评:本题考查椭圆的性质和标准方程,考查了计算能力的分类讨论思想.属于基础题.

练习册系列答案
相关题目
 ,则它的长半轴的长是( )
,则它的长半轴的长是( ) 或1
或1