题目内容
已知D是直角△ABC斜边BC上一点,AB=AD,∠ABC=β.且AC=
DC,则β=
.
| 3 |
| π |
| 3 |
| π |
| 3 |
分析:根据正弦定理可求得sinβ=
sinα,通过三角形是直角三角形,推出sinα+cos2β=0,即可求解sinβ,进而求得β的值.
| 3 |
解答: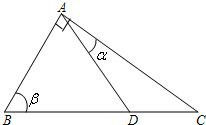 解:如图,设∠CAD=α,△ADC中,由正弦定理
解:如图,设∠CAD=α,△ADC中,由正弦定理
=
,
即
=
,则sinβ=
sinα
∵α=
-∠BAD=
-(π-2β)=2β-
得sinβ=-
cos2β=-
(1-2sin2β)
∴sinα=sin(2β-
)=-cos2β,
即sinα+cos2β=0
即2
sin2β-sinβ-
=0
解得sinβ=
或sinβ=-
∵0<β<
∴sinβ=
∴β=
,
故答案为:
 解:如图,设∠CAD=α,△ADC中,由正弦定理
解:如图,设∠CAD=α,△ADC中,由正弦定理| DC |
| sinα |
| AC |
| sin(π-β) |
即
| DC |
| sinα |
| AC |
| sinβ |
| 3 |
∵α=
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
得sinβ=-
| 3 |
| 3 |
∴sinα=sin(2β-
| π |
| 2 |
即sinα+cos2β=0
即2
| 3 |
| 3 |
解得sinβ=
| ||
| 2 |
| ||
| 3 |
∵0<β<
| π |
| 2 |
| ||
| 2 |
∴β=
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:本题主要考查了诱导公式化简求值,正弦定理.考查了学生综合分析问题和基本的运算能力.

练习册系列答案
相关题目
 DC,则β=________.
DC,则β=________.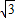 DC,则β= .
DC,则β= .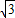 DC,则β= .
DC,则β= .