题目内容
已知函数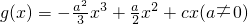 ,
,
(I)当a=1时,若函数g(x)在区间(-1,1)上是增函数,求实数c的取值范围;
(II)当 时,(1)求证:对任意的x∈[0,1],g′(x)≤1的充要条件是
时,(1)求证:对任意的x∈[0,1],g′(x)≤1的充要条件是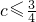 ;
;
(2)若关于x的实系数方程g′(x)=0有两个实根α,β,求证:|α|≤1,且|β|≤1的充要条件是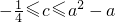 .
.
解:(I)当a=1时,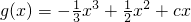 ,g'(x)=-x2+x+c,
,g'(x)=-x2+x+c,
∵g(x)在(-1,1)上为单调递增函数,∴g'(x)≥0在(-1,1)上恒成立,
∴-x2+x+c≥0在(-1,1)上恒成立,∴-1-1+c≥0,∴c≥2.
(II)设g'(x)=f(x),则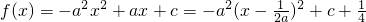 ,此抛物线关于x=
,此抛物线关于x= 对称,
对称,
由 可得,0<
可得,0< ≤1.对任意的x∈[0,1],g′(x)≤1的充要条件是它的最大值c+
≤1.对任意的x∈[0,1],g′(x)≤1的充要条件是它的最大值c+ ≤1,
≤1,
即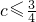 .
.
(2)关于x的实系数方程g′(x)=0 即-a2x2+ax+c=0,即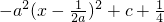 =0,
=0,
∴g′(x)=0有两个实根α,β,|α|≤1,且|β|≤1的充要条件是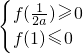 ,即
,即
 ,等价于
,等价于 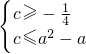 ,等价于
,等价于 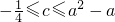 .
.
分析:(I)要使g'(x)≥0在(-1,1)上恒成立,只要它的最小值f(-1)≥0,即-1-1+c≥0,解得c≥2.
(II)设g'(x)=f(x),对任意的x∈[0,1],g′(x)≤1的充要条件是它的最大值c+ ≤1,求得c的范围.
≤1,求得c的范围.
(2)g′(x)=0有两个实根α,β,|α|≤1,且|β|≤1的充要条件是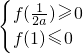 ,等价于
,等价于
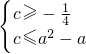 ,从而证得结论.
,从而证得结论.
点评:本题考查函数的单调性与导数的关系,二次函数在闭区间上的值域,充要条件的定义,判断g′(x)=0两个
实根α,β,|α|≤1,且|β|≤1的充要条件是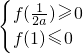 ,是解题的难点.
,是解题的难点.
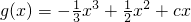 ,g'(x)=-x2+x+c,
,g'(x)=-x2+x+c,∵g(x)在(-1,1)上为单调递增函数,∴g'(x)≥0在(-1,1)上恒成立,
∴-x2+x+c≥0在(-1,1)上恒成立,∴-1-1+c≥0,∴c≥2.
(II)设g'(x)=f(x),则
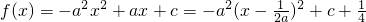 ,此抛物线关于x=
,此抛物线关于x= 对称,
对称,由
 可得,0<
可得,0< ≤1.对任意的x∈[0,1],g′(x)≤1的充要条件是它的最大值c+
≤1.对任意的x∈[0,1],g′(x)≤1的充要条件是它的最大值c+ ≤1,
≤1,即
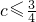 .
.(2)关于x的实系数方程g′(x)=0 即-a2x2+ax+c=0,即
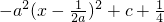 =0,
=0,∴g′(x)=0有两个实根α,β,|α|≤1,且|β|≤1的充要条件是
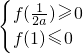 ,即
,即 ,等价于
,等价于 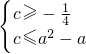 ,等价于
,等价于 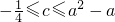 .
.分析:(I)要使g'(x)≥0在(-1,1)上恒成立,只要它的最小值f(-1)≥0,即-1-1+c≥0,解得c≥2.
(II)设g'(x)=f(x),对任意的x∈[0,1],g′(x)≤1的充要条件是它的最大值c+
 ≤1,求得c的范围.
≤1,求得c的范围.(2)g′(x)=0有两个实根α,β,|α|≤1,且|β|≤1的充要条件是
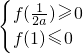 ,等价于
,等价于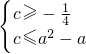 ,从而证得结论.
,从而证得结论.点评:本题考查函数的单调性与导数的关系,二次函数在闭区间上的值域,充要条件的定义,判断g′(x)=0两个
实根α,β,|α|≤1,且|β|≤1的充要条件是
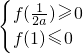 ,是解题的难点.
,是解题的难点. 
练习册系列答案
相关题目
 .
. ,
, .
. 。
。 的解集;
的解集;