题目内容
如图,在四棱锥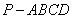 中,
中,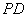
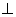 平面
平面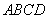 ,
,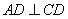 ,
,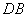 平分
平分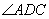 ,
,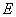 为的
为的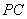 中点,
中点,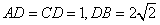
(1)证明: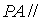 平面
平面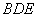
(2)证明: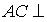 平面
平面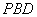
(3)求直线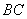 与平面
与平面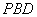 所成角的正切值
所成角的正切值
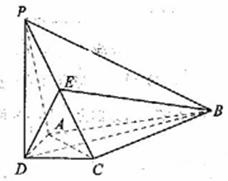
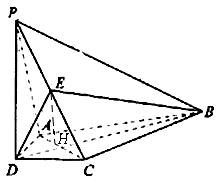 ①证明:设AC∩BD=H,连结EH,在△ADC中,
①证明:设AC∩BD=H,连结EH,在△ADC中,
因为AD=CD,且DB平分∠ADC,所以H为AC的中点,
又E为P的中点,故EH//PA
又EH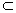 平面BDE
平面BDE
PA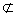 平面BDE
平面BDE
∴PA//平面BDE
②证明:∵PD⊥平面ABCD
AC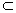 平面ABCD,所以PD⊥AC
平面ABCD,所以PD⊥AC
由(1)知,BD⊥AC,PD∩BD=D
∴AC⊥平面PBD
③解由AC⊥平面PBD可知,BH为BC在平面PBD内的射影,所以∠CBH为直线与平面PBD所成的角。
由AD⊥CD,AD=CD=1,DB=2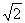
可得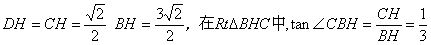

练习册系列答案
相关题目
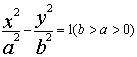 的半焦距为
的半焦距为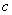 ,直线
,直线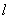 过
过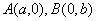 两点,若原点
两点,若原点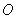 到
到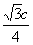 ,则双曲线的离心率为
,则双曲线的离心率为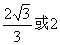 B.
B. 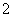 C.
C. 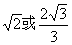 D.
D. 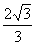
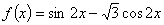 的图象( )
的图象( )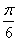 个单位 B.向左平移
个单位 B.向左平移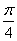 个单位 D.向左平移
个单位 D.向左平移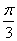 个单位
个单位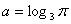 ,
,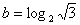 ,
,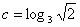 ,则( )
,则( ) B.
B.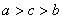
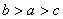 D.
D.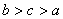
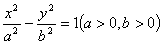 的左顶点与抛物线
的左顶点与抛物线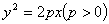 的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为
的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为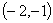 ,则双曲线的焦距为
,则双曲线的焦距为  为真命题”是命题:“
为真命题”是命题:“ 为真命题”的( )
为真命题”的( ) ,若直线上存在点
,若直线上存在点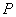 ,使得
,使得 则称该直线为“
则称该直线为“ ”.给出下列直线:①
”.给出下列直线:① ,②
,② ,③
,③ ,则这三条直线中有( )条“
,则这三条直线中有( )条“ ,且
,且 ∥
∥ ,则锐角α的余弦值为( )
,则锐角α的余弦值为( ) B.
B.  C.
C. D.
D. 
 是两个不同平面,给出四个命题:
是两个不同平面,给出四个命题: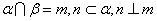 ,则
,则 ②若
②若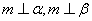 ,则
,则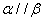
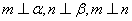 ,则
,则 ,则
,则